Séance 5 - Dérivation et étude des fonctions (Partie 2)

Sommaire

I- Applications de la fonction dérivée première

1-1/ La monotonie d’une fonction et le signe de sa fonction dérivée

1-2/ Extremums d’une fonction dérivable

II- Applications de la fonction dérivée seconde

2-1/ Position relative de la tangente et la courbe – la concavité

2-2/ Points d’inflexions

III- Centre de symétrie – axe de symétrie de la courbe d’une fonction

3-1/ Centre de symétrie de la courbe d’une fonction

3-2/ Axe de symétrie de la courbe d’une fonction

IV- Branches infinies d’une fonction

4-1/ Branches infinies

4-2/ Asymptote verticale

4-3/ Asymptote horizontale

4-4/ Asymptote oblique

V- Bilan des branches infinies

VI- Exercices

6-1/ Exercice 1

6-2/ Exercice 2

6-3/ Exercice 3

6-4/ Exercice 4

6-5/ Exercice 5

6-6/ Exercice 6

I- Applications de la fonction dérivée première

1-1/ La monotonie d’une fonction et le signe de sa fonction dérivée

Propriété

$f$ est une fonction dérivable sur un intervalle $I$

Si la fonction dérivée $f\text{'}$ est strictement positive sur $I$, alors la fonction $f$ est strictement croissante sur $I$.
(même si $f\text{'}$ s’annule en un points fini de $I$, ça ne change pas la monotonie de $f$)

Si la fonction dérivée $f\text{'}$ est strictement négative sur $I$, alors la fonction $f$ est strictement décroissante sur $I$.
(même si $f\text{'}$ s’annule en un points fini de $I$, ça ne change pas la monotonie de $f$)

Si la fonction $f\text{'}$ est nulle sur $I$ tout entier, alors $f$ est constante.

Exemple

I- Applications de la fonction dérivée première

1-2/ Extremums d’une fonction dérivable

Propriété 1

$f$ est une fonction dérivable sur un intervalle ouvert $I$, $a$ est un élément de $I$.
 
Si $f$ est dérivable au point $a$ et admet un extremum au point $a$ alors $f\text{'}\left(a\right)=0$.

Remarque

$f\text{'}\left(a\right)=0$ ne signifie pas que $f\left(a\right)$ est un extremum de la fonction $f$.

Exemple

I- Applications de la fonction dérivée première

1-2/ Extremums d’une fonction dérivable

Propriété 2

$f$ est une fonction dérivable sur un intervalle ouvert $I$, $a$ est un élément de $I$.

Si $f\text{'}$ s’annule au point $a$ et $f\text{'}$ change de signe au voisinage de $a$ alors $f\left(a\right)$ est un extremum de la fonction $f$.

Exemple

II- Applications de la fonction dérivée seconde

2-1/ Position relative de la tangente et la courbe – la concavité

Propriété et définition

$f$ est une fonction deux fois dérivable sur un intervalle $I$.
 
Si $\forall x\in I : f"\left(x\right)>0$, alors la courbe $\left({\mathcal{C}}_f\right)$ est située au dessus des tangentes des points $x$ tel que $x\in I$.

Dans ce cas on dit que la courbe $\left({\mathcal{C}}_f\right)$ de $f$ est convexe (ou sa concavité est dans le sens des ordonnés positives. On note ).

Si $\forall x\in I : f"\left(x\right)<0$, alors la courbe $\left({\mathcal{C}}_f\right)$ est située au dessous des tangentes des points $x$ tel que $x\in I$.

Dans ce cas on dit que la courbe $\left({\mathcal{C}}_f\right)$ de $f$ est concave (ou sa concavité est dans le sens des ordonnés négatives. On note ).

Exemple

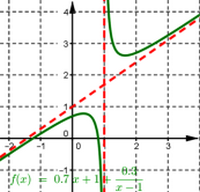
II- Applications de la fonction dérivée seconde

2-2/ Points d’inflexions

Propriété et définition

$f$ est une fonction deux fois dérivable sur un intervalle $I$, et $x_0\in I$.

Si la fonction dérivée seconde $f"$ s’annule en $x_0$ et $f"$ change de signe au voisinage de $x_0$, alors le point $A\left(x_0,f\left(x_0\right)\right)$ est un point d’inflexion au courbe $\left({\mathcal{C}}_f\right)$.

Dans ce cas la tangente au point $A\left(x_0,f\left(x_0\right)\right)$ coupe (ou traverse) la courbe $\left({\mathcal{C}}_f\right)$.

Exemple

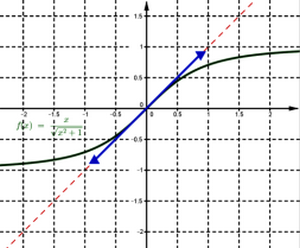
III- Centre de symétrie – axe de symétrie de la courbe d’une fonction

3-1/ Centre de symétrie de la courbe d’une fonction

Propriété

Soit $\left({\mathcal{C}}_f\right)$ la courbe représentative d’une fonction définie sur $D_f$ dans un plan $\left(P\right)$ rapporté à un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$.

Le point $I\left(a,b\right)$ est centre de symétrie de la courbe $\left({\mathcal{C}}_f\right)\iff \left\{\begin{array}{l}\forall x\in D_f ; 2a-x\in D_f\\ \forall x\in D_f ; f\left( 2a-x\right)+f\left(x\right)=2b\end{array}\right.$

Exemple

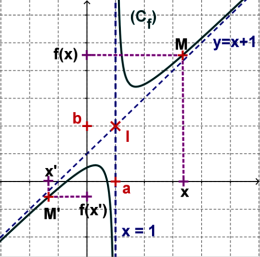
III- Centre de symétrie – axe de symétrie de la courbe d’une fonction

3-2/ Axe de symétrie de la courbe d’une fonction

Propriété

Soit $\left({\mathcal{C}}_f\right)$ la courbe représentative d’une fonction définie sur $D_f$ dans un plan $\left(P\right)$ rapporté à un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$.

La droite d’équation $D : x=a$ est axe de symétrie de la courbe $\left({\mathcal{C}}_f\right)\iff \left\{\begin{array}{l}\forall x\in D_f ; 2a-x\in D_f\\ \forall x\in D_f ; f\left( 2a-x\right)=f\left(x\right)\end{array}\right.$

Exemple

IV- Branches infinies d’une fonction

4-1/ Branches infinies

Définition

Soit $\left({\mathcal{C}}_f\right)$ la courbe représentative d’une fonction définie sur $D_f$ dans un plan $\left(P\right)$ rapporté à un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$.

Si au moins une des coordonnées d’un point $M$ de la courbe de $\left({\mathcal{C}}_f\right)$ tend vers l’infinie, on dit que la courbe $\left({\mathcal{C}}_f\right)$ admet une branche infinie.

Exemple

IV- Branches infinies d’une fonction

4-2/ Asymptote verticale

Définition

Soit $\left({\mathcal{C}}_f\right)$ la courbe représentative d’une fonction définie sur $D_f$ dans un plan $\left(P\right)$ rapporté à un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$.

Si $\underset{x\to a^{+}}{\lim }f\left(x\right)=\pm \infty$ et $\underset{x\to a^{-}}{\lim }f\left(x\right)=\pm \infty$, alors la droite d’équation $x=a$ est une asymptote verticale à $\left({\mathcal{C}}_f\right)$ (à droite de $a$ ou à gauche de $a$).

Exemple

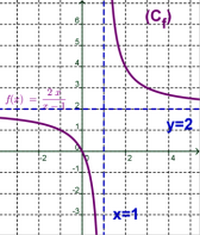
IV- Branches infinies d’une fonction

4-3/ Asymptote horizontale

Définition

Soit $\left({\mathcal{C}}_f\right)$ la courbe représentative d’une fonction définie sur $D_f$ dans un plan $\left(P\right)$ rapporté à un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$.

Si $\underset{x\to +\infty }{\lim }f\left(x\right)=b$ (ou $\underset{x\to -\infty }{\lim }f\left(x\right)=c$), alors la droite d’équation $y=b$ (ou $y=c$) est une asymptote horizontale à $\left({\mathcal{C}}_f\right)$ au voisinage de $+\infty$ (ou $-\infty$)

Exemple

IV- Branches infinies d’une fonction

4-4/ Asymptote oblique

Définition

Soit $\left({\mathcal{C}}_f\right)$ la courbe représentative d’une fonction définie sur $D_f$ (tel que $]a,+\infty [\subset D_f$ ou $]-\infty ,a[\subset D_f$)dans un plan $\left(P\right)$ rapporté à un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$.

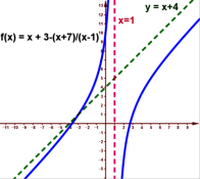
Si $\underset{x\to \pm \infty }{\lim }f\left(x\right)-\left(ax+b\right)=0$ , alors la droite d’équation $y=ax+b$ est une asymptote oblique à $\left({\mathcal{C}}_f\right)$ au voisinage de $\pm \infty$.

Exemple

IV- Branches infinies d’une fonction

4-4/ Asymptote oblique

Propriétés

Si la droite d’équation $y=ax+b$ est une asymptote oblique à $\left({\mathcal{C}}_f\right)$ au voisinage de$\pm \infty$ , donc pour déterminer $a$ et $b$ on calcule les limites suivantes :

Pour déterminer $a$ on calcule $\underset{x\to \pm \infty }{\lim }\frac{f\left(x\right)}{x}=a\in \mathrm{ℝ}*$

Pour déterminer $b$ on calcule $\underset{x\to \pm \infty }{l\mathrm{im}}\left(f\left(x\right)-ax\right)=b\in \mathrm{ℝ} \left(b\ne \pm \infty \right)$

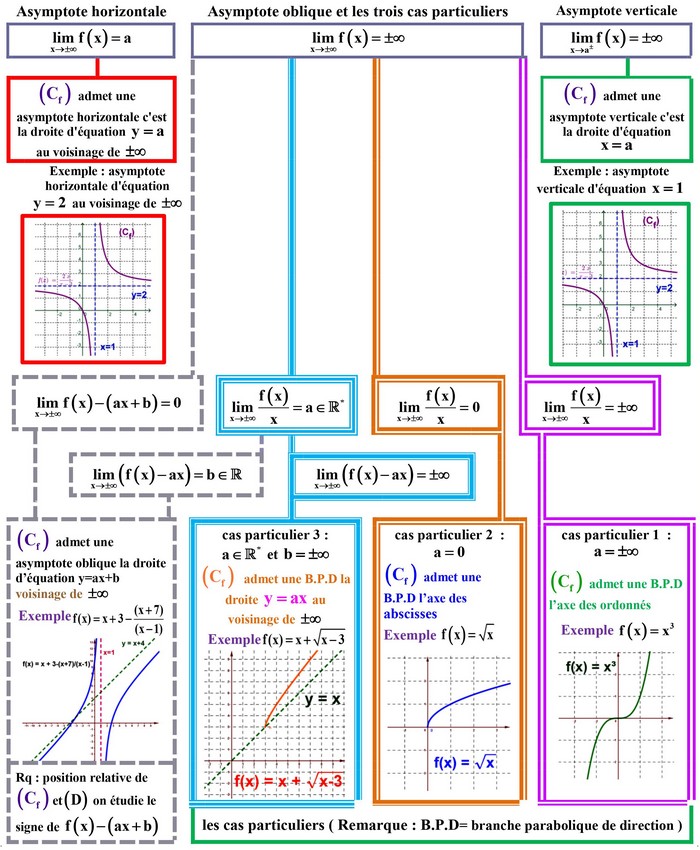
Les cas particuliers :

• 1er cas particulier : $a=\pm \infty$, on dit que $\left({\mathcal{C}}_f\right)$ admet une branche parabolique de direction l’axe des ordonnés.
• 2nd cas particulier : $a=0$, on dit que $\left({\mathcal{C}}_f\right)$ admet une branche parabolique de direction  l’axe des abscisses .
• 3ème cas particulier : $b=\pm \infty$ avec $a\in \mathrm{ℝ}*$, on dit que $\left({\mathcal{C}}_f\right)$ admet une branche parabolique de direction la droite d’équation $y=ax$.

Exemples

V- Bilan des branches infinies

VI- Exercices

6-1/ Exercice 1

On considère la fonction numérique $f$ définie par $f\left(x\right)=x+\frac{2}{\sqrt{x+1}}$, et soit $\left({\mathcal{C}}_f\right)$ sa courbe représentative dans un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$ (unité de 1 cm).

a- Déterminer $D_f$ le domaine de définition de la fonction $f$.

b- Calculer $\underset{x\to +\infty }{\lim }f\left(x\right)$ et $\underset{x\to -1^{+}}{\lim }f\left(x\right)$, puis interpréter géométriquement le deuxième résultat.

c- Montrer que la courbe $\left({\mathcal{C}}_f\right)$ admet une asymptote oblique $\left(\Delta \right)$ au voisinage de $+\infty$ dont on déterminera son équation.

d- Étudier la position relative de la courbe $\left({\mathcal{C}}_f\right)$ et la droite $\left(\Delta \right)$.

a- Montrer que $f\text{'}\left(x\right)=1-\frac{1}{\left(x+1\right)\sqrt{x+1}}$ pour tout $x$ de $D_f$.

b- Montrer que pour tout $x$ de $]-1,0]$ on a $\frac{1}{\left(x+1\right)\sqrt{x+1}}\ge 1$, puis en déduire le signe de $f\text{'}\left(x\right)$ sur $]-1,0]$.

c- Montrer que pour tout $x$ de $[0,+\infty [$ on a $\frac{1}{\left(x+1\right)\sqrt{x+1}}\le 1$, puis en déduire le signe de $f\text{'}\left(x\right)$ sur $[0,+\infty [$.

d- Dresser le tableau de variations de la fonction $f$ sur $D_f$.

e- Donner l’équation de la tangente $\left(T\right)$ à la courbe $\left({\mathcal{C}}_f\right)$ au point $x_0=0$.

4. Construire la droite $\left(\Delta \right)$ et la tangente $\left(T\right)$ et la courbe $\left({\mathcal{C}}_f\right)$ de $f$ dans le même repère $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$.

a- Montrer que la fonction $f$ admet une fonction réciproque $f^{-1}$ définie sur l’intervalle $J$ qu'on déterminera.

b- Montrer que la fonction réciproque $f^{-1}$ est dérivable sur l’intervalle $J$.

c- Construire dans le même repère $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$ la courbe représentative $\left({\mathcal{C}}_{f^{-1}}\right)$ de la fonction $f^{-1}$.

VI- Exercices

6-2/ Exercice 2

On considère la fonction numérique $f$ définie par $f\left(x\right)=\frac{x-1}{\sqrt{x^2-2x+2}}$, et soit $\left({\mathcal{C}}_f\right)$ sa courbe représentative dans un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$ (unité de 2 cm).

a- Montrer que $f$ est définie sur $D_f=\mathrm{ℝ}$.

b- Calculer $\underset{x\to +\infty }{\lim }f\left(x\right)$ et $\underset{x\to -\infty }{\lim }f\left(x\right)$, puis interpréter géométriquement les deux résultats.

a- Montrer que $f\text{'}\left(x\right)=\frac{1}{\left(x^2-2x+2\right)\sqrt{x^2-2x+2}}$ pour tout $x$ de $\mathrm{ℝ}$.

b- Montrer que la fonction $f$ est croissante sur $D_f$.

c- Dresser le tableau de variations de la fonction $f$ sur $\mathrm{ℝ}$.

a- Montrer que le point $I\left(1;0\right)$ est un centre de symétrie de la courbe $\left({\mathcal{C}}_f\right)$.

b- Donner l’équation de la tangente $\left(T\right)$ à la courbe $\left({\mathcal{C}}_f\right)$ au point $I$.

4. Construire la tangente $\left(T\right)$ et la courbe $\left({\mathcal{C}}_f\right)$ de $f$ dans le même repère $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$.

a- Montrer que la fonction $f$ admet une fonction réciproque $f^{-1}$ définie sur l’intervalle $J$ qu'on déterminera.

b- Construire dans le même repère $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$ la courbe représentative $\left({\mathcal{C}}_{f^{-1}}\right)$ de la fonction $f^{-1}$.

c- Calculer $f\left(1\right)$, puis montrer que la fonction réciproque $f^{-1}$ est dérivable en $0$ puis calculer ${\left(f^{-1}\right)}^{\text{'}}\left(0\right)$.

VI- Exercices

6-3/ Exercice 3

On considère la fonction numérique $f$ définie sur $[0,+\infty [$ par $\left\{\begin{array}{l}f\left(x\right)=\frac{\sqrt{x}-1}{x-1} ; x\in [0,1[\cup ]1,+\infty [\\ f\left(1\right)=\frac{1}{2}\end{array}\right.$

Soit $\left({\mathcal{C}}_f\right)$ sa courbe représentative dans un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$ (unité de 2 cm).

a- Calculer $\underset{x\to +\infty }{\lim }f\left(x\right)$, puis interpréter géométriquement le résultat.

b- Étudier la continuité de la fonction $f$ au point $x_0=1$.

a- Montrer que la fonction $f$ est dérivable au point $x_0=1$ et le nombre dérivé est $f\text{'}\left(1\right)=-\frac{1}{8}$.

b- Donner l’équation de la tangente $\left(T\right)$ à la courbe $\left({\mathcal{C}}_f\right)$ au point $x_0=1$.

c- Étudier la dérivabilité à droite de la fonction $f$ au point $x_0=0$.

d- Vérifier la fonction dérivée de $f$ sur $]0,+\infty [/\left\{1\right\}$ est $f\text{'}\left(x\right)=\frac{-{\left(\sqrt{x}-1\right)}^2}{2\sqrt{x}{\left(x-1\right)}^2}$.

e- Dresser le tableau de variations de la fonction $f$ sur $[0,+\infty [$.

3. Construire la courbe $\left({\mathcal{C}}_f\right)$ de $f$ dans le repère $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$.

On considère $g$ la restriction de la fonction $f$ sur $I=[0,+\infty [$.

4) a- Montrer que la fonction $g$ admet une fonction réciproque $g^{-1}$ définie sur l’intervalle $J$ qu'on déterminera.

4) b- Calculer $g\left(4\right)$ puis montrer que la fonction réciproque $g^{-1}$ est dérivable en $\frac{1}{3}$ puis calculer ${\left(g^{-1}\right)}^{\text{'}}\left(\frac{1}{3}\right)$.

VI- Exercices

6-4/ Exercice 4

On considère la fonction numérique $f$ définie sur $D_f=]-\infty ,-1[\cup ]-1,+\infty [$ par :

$\left\{\begin{array}{l}f\left(x\right)=\frac{x^4}{x^3+x^2} ; x\ne -1 et x\ne 0\\ f\left(0\right)=0\end{array}\right.$

Soit $\left({\mathcal{C}}_f\right)$ la courbe représentative de la fonction  dans un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$ (unité de 1 cm).

a- Calculer $\underset{x\to -1^{-}}{\lim }f\left(x\right)$ et $\underset{x\to -1^{+}}{\lim }f\left(x\right)$ puis interpréter géométriquement les résultats.

b- Calculer $\underset{x\to +\infty }{\lim }f\left(x\right)$ et $\underset{x\to +\infty }{\lim }f\left(x\right)-\left(x-1\right)$ puis interpréter géométriquement les résultats.

c- Calculer $\underset{x\to -\infty }{\lim }f\left(x\right)$.

d- Montrer que $\left({\mathcal{C}}_f\right)$ admet au voisinage de $-\infty$ une asymptote oblique au voisinage de $-\infty$ dont on déterminera l’équation.

e- Étudier la position relative de la courbe $\left({\mathcal{C}}_f\right)$ et la droite $\left(D\right)$ d’équation $y=x-1$ sur $D_f$.

a- Calculer $\underset{x\to 0}{\lim }\frac{f\left(x\right)}{x}$ puis interpréter géométriquement le résultat.

b- Calculer $f\text{'}\left(x\right)$ pour tout $x$ de $]-\infty ,-1[\cup ]-1,0[\cup ]0,+\infty [$, puis vérifier que $f\text{'}\left(x\right)=\frac{x^5\left(x+2\right)}{{\left(x^3+x^2\right)}^2}$.

c- Étudier le signe de$f\text{'}\left(x\right)$  sur $]-\infty ,-1[\cup ]-1,0[\cup ]0,+\infty [$.

d- Dresser le tableau de variations de la fonction $f$ sur $D_f$.

e- Écrire l’équation réduite de la tangente à $\left({\mathcal{C}}_f\right)$ au point $x_0=0$.

3. Construire dans le repère $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$ la droite $\left(D\right)$ et la courbe $\left({\mathcal{C}}_f\right)$ (unité de 1 cm).

On considère $g$ la restriction de la fonction $f$ sur $I=]-1,0]$.

4) a- Montrer que la fonction $g$ admet une fonction réciproque $g^{-1}$ définie sur l’intervalle $J$ qu'on déterminera.

4) b- Calculer $g\left(\frac{1}{2}\right)$ puis montrer que la fonction réciproque $g^{-1}$ est dérivable en $\frac{1}{6}$.

4) c- Calculer ${\left(g^{-1}\right)}^{\text{'}}\left(\frac{1}{6}\right)$.

VI- Exercices

6-5/ Exercice 5

Soit la fonction : $f\left(x\right)=\frac{x\left(x^2+1\right)}{x^2-1}$

Soit $\left({\mathcal{C}}_f\right)$ sa représentation graphique dans un repère orthonormé du plan $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$.

1. Déterminer $D_f$, puis étudier la continuité et la dérivabilité de $f$ sur $D_f$. Justifier les réponses.

2. Étudier la parité de $f$ et en déduire un élément de symétrie de $\left({\mathcal{C}}_f\right)$.

3. Étudier les limites de $f$ aux bornes de $D_f$, et en déduire les asymptotes éventuelles à $\left({\mathcal{C}}_f\right)$.

4. Étudier les variations de $f$ et dresser son tableau de variations.

5. Étudier la concavité de $\left({\mathcal{C}}_f\right)$ et résumer cette étude dans un tableau.

6. Déterminer une équation cartésienne de la tangente $\left(T\right)$ à $\left({\mathcal{C}}_f\right)$ au point d’abscisse $0$.

7. Étudier la position de $\left({\mathcal{C}}_f\right)$ par rapport à $\left(T\right)$.

8. Tracer $\left({\mathcal{C}}_f\right)$ et $\left(T\right)$ dans le repère $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$.

VI- Exercices

6-5/ Exercice 6

Partie 1

Soit $g$ la fonction définie sur $\mathrm{ℝ}$ par : $g\left(x\right)=1+\frac{x}{\sqrt{x^2+1}}$.

1. Calculer $\underset{x\to -\infty }{\lim }g\left(x\right)$. et $\underset{x\to +\infty }{\lim }g\left(x\right)$

2. Vérifier que : $g\text{'}\left(x\right)=\frac{1}{\left(x^2+1\right)\sqrt{x^2+1}}$.

3. En déduire que : $\left(\forall x\in \mathrm{ℝ}\right); g\left(x\right)>0$.

Partie 2

Soit $f$ la fonction définie sur $\mathrm{ℝ}$ par : $f\left(x\right)=x-1+\sqrt{x^2+1}$.

1. Vérifier que pour tout réel $x$ on a : $f\text{'}\left(x\right)=g\left(x\right)$.

2. Dresser le tableau de variation de $f$.

3. Montrer que $\underset{x\to -\infty }{\lim }f\left(x\right)=-1$. Interpréter graphiquement le résultat obtenu.

4. Montrer que la droite $\left(D\right) : y=2x-1$ est une asymptote oblique à $\left({\mathcal{C}}_f\right)$ au voisinage de $+\infty$.

5. Tracer $\left({\mathcal{C}}_f\right)$ et $\left(D\right)$ dans un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$.