
Mathématiques : 2 Bac SPC-SVT-STE-STM
Séance 4 (Dérivation et étude des fonctions – Partie 1)
Professeur : Mr CHEDDADI Haitam
Sommaire
I- Dérivabilité d’une fonction en un point – Dérivabilité à droite et à gauche en un point
1-1/ Dérivabilité
1-2/ Interprétation géométrique des nombres dérivées et et
II- Dérivabilité sur un intervalle
III- La fonction dérivée première d’une fonction – la fonction dérivée seconde – dérivée nième d’ une fonction
IV- Les opérations sur les fonctions dérivables
V- Dérivabilité des fonctions polynomiales, rationnelles, trigonométriques et
VI- Dérivabilité de la composée de deux fonctions
VII- La fonction dérivée de la fonction réciproque
IIX- Tableau des fonctions dérivées des fonctions usuelles
IX- Exerccies
9-1/ Exerccie 1
9-2/ Exerccie 2
9-3/ Exerccie 3
9-4/ Exerccie 4
9-5/ Exerccie 5
9-6/ Exerccie 6
I- Dérivabilité d’une fonction en un point – Dérivabilité à droite et à gauche en un point
1-1/ Dérivabilité
Définitions
Soit une fonction tel que son domaine de définition contient un intervalle ouvert et
est dérivable au point
s’appelle le nombre dérivé de en
est dérivable à droite de
s’appelle le nombre dérivé à gauche de en
est dérivable à gauche de
s’appelle le nombre dérivé à gauche de en
Exemple
I- Dérivabilité d’une fonction en un point – Dérivabilité à droite et à gauche en un point
1-1/ Dérivabilité
Propriété
Soit une fonction
est dérivable au point est dérivable à droite et à gauche et
Exemple
I- Dérivabilité d’une fonction en un point – Dérivabilité à droite et à gauche en un point
1-2/ Interprétation géométrique des nombres dérivées et et
Interprétation géométrique des nombres dérivées
est une fonction dérivable au point .
sa courbe représentative dans un repère .
Le nombre dérivé est le coefficient directeur de la droite tangente à la courbe au point (le point ).
L'équation cartésienne de la tangente à la courbe au point est .
Si alors la tangente est parallèle à l’axe des abscisses.
Exemple
I- Dérivabilité d’une fonction en un point – Dérivabilité à droite et à gauche en un point
1-2/ Interprétation géométrique des nombres dérivées et et
Interprétation géométrique des nombres dérivées et
Si est dérivable à droite de , alors on a une demi-tangente à droite de de coefficient directeur .
L'équation de la demi tangente à droite de est avec .
Si est dérivable à gauche de , alors on a une demi-tangente à gauche de de coefficient directeur .
L'équation de la demi tangente à gauche de est avec .
Si , alors n’est pas dérivable en et le point est appelé point anguleux.
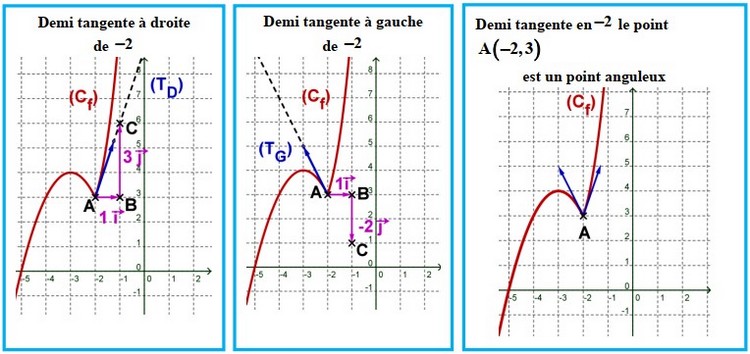
Exemple
I- Dérivabilité d’une fonction en un point – Dérivabilité à droite et à gauche en un point
1-2/ Interprétation géométrique des nombres dérivées et et
Remarque
Si n’est pas dérivable à droite (c.à.d. ), dans ce cas on a une demi tangente à droite de parallèle à l’axe des ordonnées.
Si n’est pas dérivable à gauche (c.à.d. ), dans ce cas on a demi tangente à gauche de parallèle à l’axe des ordonnées.
Exemple
II- Dérivabilité sur un intervalle
Définitions
est une fonction dérivable sur est dérivable en tout point de .
est une fonction dérivable sur est dérivable sur et est dérivable à droite du point .
est une fonction dérivable sur est dérivable sur et est dérivable à gauche du point .
est une fonction dérivable sur est dérivable sur et est dérivable à droite de et à gauche de .
Exemple
III- La fonction dérivée première d’une fonction – la fonction dérivée seconde – dérivée nième d’ une fonction
Définitions
est une fonction dérivable sur un intervalle .
La fonction qui relie chaque élément de par le nombre s’appelle la fonction dérivée de et on note .
s’appelle la fonction dérivée de .
La fonction dérivée de sur s’appelle la fonction dérivée seconde (dérivée d’ordre 2), on la note ou .
En général : la dérivée d’ordre de est la fonction dérivée de (la dérivée de la fonction dérivée d’ordre ), et on note .
Exemple
IV- Les opérations sur les fonctions dérivables
Propriété
Soient et deux fonctions dérivables sur .
On a :
La fonction est dérivable sur et
La fonction est dérivable sur et
La fonction est dérivable sur et
La fonction est dérivable sur et
La fonction est dérivable sur et
Exemple
V- Dérivabilité des fonctions polynomiales, rationnelles, trigonométriques et
Propriété
Toute fonction polynomiale est dérivable sur son ensemble de définition et .
Toute fonction rationnelle est dérivable sur son ensemble de définition .
est une fonction dérivable sur un intervalle :
La fonction avec est dérivable sur et on a .
Si pour tout , on a la fonction avec est dérivable sur et .
La fonction est dérivable sur avec .
La fonction est dérivable sur avec .
La fonction est dérivable sur avec
Exemple
VI- Dérivabilité de la composée de deux fonctions
Propriété
Si est dérivable en et est dérivable en , alors la fonction est dérivable en et on a :
Application
Exemple
VII- La fonction dérivée de la fonction réciproque
Théorème
Si est dérivable en et , alors la fonction est dérivable en
et
ou encore
Application:
Exemple
IIX- Tableau des fonctions dérivées des fonctions usuelles

IX- Exerccies
9-1/ Exerccie 1
- Dans chacun des cas suivantes, étudier la dérivabilité de la fonction en et interpréter le résultat graphiquement :
IX- Exerccies
9-2/ Exerccie 2
- Déterminer la fonction dérivée de la fonction dans chacun des cas suivants :
IX- Exerccies
9-3/ Exerccie 3
- Déterminer la fonction dérivée de la fonction dans chacun des cas suivants :
IX- Exerccies
9-4/ Exerccie 4
On considère la fonction numérique définie par :
- Déterminer le domaine de définition de la fonction .
- Calculer et et .
- Étudier la dérivabilité à gauche de au point puis interpréter le résultat graphiquement.
- Calculer , puis interpréter le résultat graphiquement.
- Montrer que pour tout de on a puis déterminer son signe sur .
- Calculer pour tout de puis déterminer son signe sur .
- Dresser le tableau de variations de la fonction sur .
Soit la restriction de la fonction à l’intervalle .
- Montrer que la restriction admet une fonction réciproque définie sur l’intervalle qu’on déterminera.
- Calculer et .
IX- Exerccies
9-5/ Exerccie 5
Soit la fonction définie sur par :
- Calculer et .
- Est-ce que la fonction est continue en ?
- Étudier la continuité de sur .
- Étudier la dérivabilité de en , et interpréter géométriquement les résultats.
IX- Exerccies
9-6/ Exerccie 6
On considère la fonction numérique définie par :
- Montrer que l’équation une seule solution sur , et que .
- Donner un encadrement d’amplitude de .
- En déduire que et .
- Montrer que admet une fonction réciproque définie sur un intervalle que l’on précisera.
- Calculer , et .


