
Mathématiques : 2 Bac SPC-SVT-STE-STM
Séance 5 (Dérivation et étude des fonctions – Partie 2)
Professeur : Mr CHEDDADI Haitam
Sommaire
I- Applications de la fonction dérivée première
1-1/ La monotonie d’une fonction et le signe de sa fonction dérivée
1-2/ Extremums d’une fonction dérivable
II- Applications de la fonction dérivée seconde
2-1/ Position relative de la tangente et la courbe – la concavité
2-2/ Points d’inflexions
III- Centre de symétrie – axe de symétrie de la courbe d’une fonction
3-1/ Centre de symétrie de la courbe d’une fonction
3-2/ Axe de symétrie de la courbe d’une fonction
IV- Branches infinies d’une fonction
4-1/ Branches infinies
4-2/ Asymptote verticale
4-3/ Asymptote horizontale
4-4/ Asymptote oblique
V- Bilan des branches infinies
VI- Exercices
6-1/ Exercice 1
6-2/ Exercice 2
6-3/ Exercice 3
6-4/ Exercice 4
6-5/ Exercice 5
6-6/ Exercice 6
I- Applications de la fonction dérivée première
1-1/ La monotonie d’une fonction et le signe de sa fonction dérivée
Propriété
f est une fonction dérivable sur un intervalle I
Si la fonction dérivée f' est strictement positive sur , alors la fonction est strictement croissante sur .
(même si s’annule en un points fini de , ça ne change pas la monotonie de )
Si la fonction dérivée est strictement négative sur , alors la fonction est strictement décroissante sur .
(même si s’annule en un points fini de , ça ne change pas la monotonie de )
Si la fonction est nulle sur tout entier, alors est constante.
Exemple
I- Applications de la fonction dérivée première
1-2/ Extremums d’une fonction dérivable
Propriété 1
est une fonction dérivable sur un intervalle ouvert , est un élément de .
Si est dérivable au point et admet un extremum au point alors .
Remarque
ne signifie pas que est un extremum de la fonction .
Exemple

I- Applications de la fonction dérivée première
1-2/ Extremums d’une fonction dérivable
Propriété 2
est une fonction dérivable sur un intervalle ouvert , est un élément de .
Si s’annule au point et change de signe au voisinage de alors est un extremum de la fonction .
Exemple
II- Applications de la fonction dérivée seconde
2-1/ Position relative de la tangente et la courbe – la concavité
Propriété et définition
est une fonction deux fois dérivable sur un intervalle .
Si , alors la courbe est située au dessus des tangentes des points tel que .
Dans ce cas on dit que la courbe de est convexe (ou sa concavité est dans le sens des ordonnés positives. On note  ).
).
Si , alors la courbe est située au dessous des tangentes des points tel que .
Dans ce cas on dit que la courbe de est concave (ou sa concavité est dans le sens des ordonnés négatives. On note  ).
).
Exemple
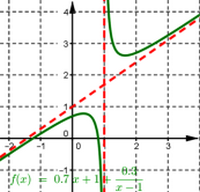
II- Applications de la fonction dérivée seconde
2-2/ Points d’inflexions
Propriété et définition
est une fonction deux fois dérivable sur un intervalle , et .
Si la fonction dérivée seconde s’annule en et change de signe au voisinage de , alors le point est un point d’inflexion au courbe .
Dans ce cas la tangente au point coupe (ou traverse) la courbe .
Exemple
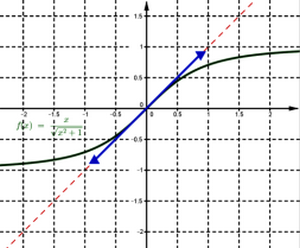
III- Centre de symétrie – axe de symétrie de la courbe d’une fonction
3-1/ Centre de symétrie de la courbe d’une fonction
Propriété
Soit la courbe représentative d’une fonction définie sur dans un plan rapporté à un repère orthonormé .
Le point est centre de symétrie de la courbe
Exemple
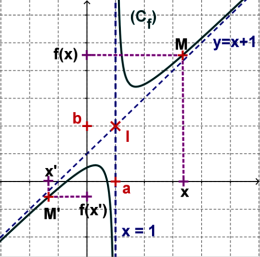
III- Centre de symétrie – axe de symétrie de la courbe d’une fonction
3-2/ Axe de symétrie de la courbe d’une fonction
Propriété
Soit la courbe représentative d’une fonction définie sur dans un plan rapporté à un repère orthonormé .
La droite d’équation est axe de symétrie de la courbe
Exemple

IV- Branches infinies d’une fonction
4-1/ Branches infinies
Définition
Soit la courbe représentative d’une fonction définie sur dans un plan rapporté à un repère orthonormé .
Si au moins une des coordonnées d’un point de la courbe de tend vers l’infinie, on dit que la courbe admet une branche infinie.
Exemple
IV- Branches infinies d’une fonction
4-2/ Asymptote verticale
Définition
Soit la courbe représentative d’une fonction définie sur dans un plan rapporté à un repère orthonormé .
Si et , alors la droite d’équation est une asymptote verticale à (à droite de ou à gauche de ).
Exemple
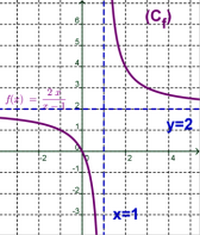
IV- Branches infinies d’une fonction
4-3/ Asymptote horizontale
Définition
Soit la courbe représentative d’une fonction définie sur dans un plan rapporté à un repère orthonormé .
Si (ou ), alors la droite d’équation (ou ) est une asymptote horizontale à au voisinage de (ou )
Exemple

IV- Branches infinies d’une fonction
4-4/ Asymptote oblique
Définition
Soit la courbe représentative d’une fonction définie sur (tel que ou )dans un plan rapporté à un repère orthonormé .
Si , alors la droite d’équation est une asymptote oblique à au voisinage de .
Exemple
IV- Branches infinies d’une fonction
4-4/ Asymptote oblique
Propriétés
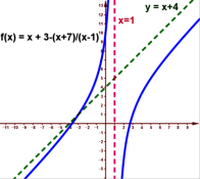
Si la droite d’équation est une asymptote oblique à au voisinage de , donc pour déterminer et on calcule les limites suivantes :
Pour déterminer on calcule
Pour déterminer on calcule
Les cas particuliers :
- 1er cas particulier : , on dit que admet une branche parabolique de direction l’axe des ordonnés.
- 2nd cas particulier : , on dit que admet une branche parabolique de direction l’axe des abscisses .
- 3ème cas particulier : avec , on dit que admet une branche parabolique de direction la droite d’équation .
Exemples
V- Bilan des branches infinies
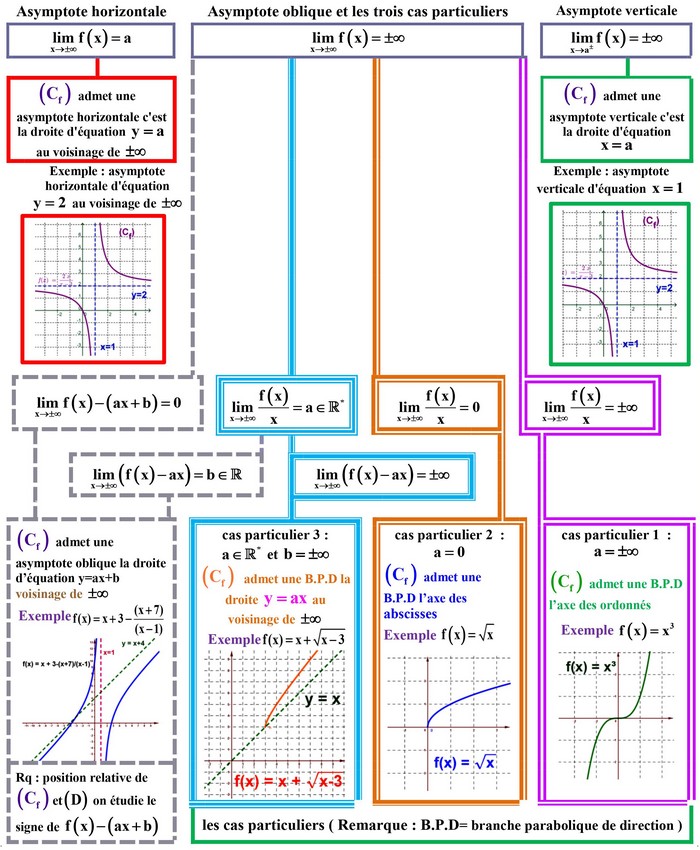
VI- Exercices
6-1/ Exercice 1
On considère la fonction numérique définie par , et soit sa courbe représentative dans un repère orthonormé (unité de 1 cm).
a- Déterminer le domaine de définition de la fonction .
b- Calculer et , puis interpréter géométriquement le deuxième résultat.
c- Montrer que la courbe admet une asymptote oblique au voisinage de dont on déterminera son équation.
d- Étudier la position relative de la courbe et la droite .
a- Montrer que pour tout de .
b- Montrer que pour tout de on a , puis en déduire le signe de sur .
c- Montrer que pour tout de on a , puis en déduire le signe de sur .
d- Dresser le tableau de variations de la fonction sur .
e- Donner l’équation de la tangente à la courbe au point .
- Construire la droite et la tangente et la courbe de dans le même repère .
a- Montrer que la fonction admet une fonction réciproque définie sur l’intervalle qu'on déterminera.
b- Montrer que la fonction réciproque est dérivable sur l’intervalle .
c- Construire dans le même repère la courbe représentative de la fonction .
VI- Exercices
6-2/ Exercice 2
On considère la fonction numérique définie par , et soit sa courbe représentative dans un repère orthonormé (unité de 2 cm).
a- Montrer que est définie sur .
b- Calculer et , puis interpréter géométriquement les deux résultats.
a- Montrer que pour tout de .
b- Montrer que la fonction est croissante sur .
c- Dresser le tableau de variations de la fonction sur .
a- Montrer que le point est un centre de symétrie de la courbe .
b- Donner l’équation de la tangente à la courbe au point .
- Construire la tangente et la courbe de dans le même repère .
a- Montrer que la fonction admet une fonction réciproque définie sur l’intervalle qu'on déterminera.
b- Construire dans le même repère la courbe représentative de la fonction .
c- Calculer , puis montrer que la fonction réciproque est dérivable en puis calculer .
VI- Exercices
6-3/ Exercice 3
On considère la fonction numérique définie sur par
Soit sa courbe représentative dans un repère orthonormé (unité de 2 cm).
a- Calculer , puis interpréter géométriquement le résultat.
b- Étudier la continuité de la fonction au point .
a- Montrer que la fonction est dérivable au point et le nombre dérivé est .
b- Donner l’équation de la tangente à la courbe au point .
c- Étudier la dérivabilité à droite de la fonction au point .
d- Vérifier la fonction dérivée de sur est .
e- Dresser le tableau de variations de la fonction sur .
- Construire la courbe de dans le repère .
On considère la restriction de la fonction sur .
4) a- Montrer que la fonction admet une fonction réciproque définie sur l’intervalle qu'on déterminera.
4) b- Calculer puis montrer que la fonction réciproque est dérivable en puis calculer .
VI- Exercices
6-4/ Exercice 4
On considère la fonction numérique définie sur par :
Soit la courbe représentative de la fonction dans un repère orthonormé (unité de 1 cm).
a- Calculer et puis interpréter géométriquement les résultats.
b- Calculer et puis interpréter géométriquement les résultats.
c- Calculer .
d- Montrer que admet au voisinage de une asymptote oblique au voisinage de dont on déterminera l’équation.
e- Étudier la position relative de la courbe et la droite d’équation sur .
a- Calculer puis interpréter géométriquement le résultat.
b- Calculer pour tout de , puis vérifier que .
c- Étudier le signe de sur .
d- Dresser le tableau de variations de la fonction sur .
e- Écrire l’équation réduite de la tangente à au point .
- Construire dans le repère la droite et la courbe (unité de 1 cm).
On considère la restriction de la fonction sur .
4) a- Montrer que la fonction admet une fonction réciproque définie sur l’intervalle qu'on déterminera.
4) b- Calculer puis montrer que la fonction réciproque est dérivable en .
4) c- Calculer .
VI- Exercices
6-5/ Exercice 5
Soit la fonction :
Soit sa représentation graphique dans un repère orthonormé du plan .
- Déterminer , puis étudier la continuité et la dérivabilité de sur . Justifier les réponses.
- Étudier la parité de et en déduire un élément de symétrie de .
- Étudier les limites de aux bornes de , et en déduire les asymptotes éventuelles à .
- Étudier les variations de et dresser son tableau de variations.
- Étudier la concavité de et résumer cette étude dans un tableau.
- Déterminer une équation cartésienne de la tangente à au point d’abscisse .
- Étudier la position de par rapport à .
- Tracer et dans le repère .
VI- Exercices
6-5/ Exercice 6
Partie 1
Soit la fonction définie sur par : .
- Calculer . et
- Vérifier que : .
- En déduire que : .
Partie 2
Soit la fonction définie sur par : .
- Vérifier que pour tout réel on a : .
- Dresser le tableau de variation de .
- Montrer que . Interpréter graphiquement le résultat obtenu.
- Montrer que la droite est une asymptote oblique à au voisinage de .
- Tracer et dans un repère orthonormé .


