PC 2Bac SVT-STE-STM - Semestre 1 Devoir 1 Modèle 1

Exercice 1 (7 pts)

Une lame vibrante en mouvement sinusoïdal de fréquence $f=10Hz$, fixée à l’extrémité $O$ d’une corde de longueur $L=3,0m$, génère le long de celle-ci une onde progressive périodique.

Un dispositif approprié empêche tout phénomène de réflexion à l’autre extrémité $O’$ de la corde.

À la date origine $t_0=0s$, on suppose que tous les points de la corde ont été atteints par l’onde.

La célérité $\nu$ de l’onde est donnée en fonction de la tension $F$ de la corde et de sa masse linéique $\mu$ (masse par unité de longueur), par la relation : $\nu =\sqrt{\frac{F}{\mu }}$

La masse linéique de la corde est : $\mu =0,10Kg.m^{-1}$

Le document suivant représente l’aspect de la corde à la date $t_1=0,50s$ :

1. L’onde étudiée est-elle transversale ou longitudinale ? Justifier votre réponse.

2. Quelle périodicité de l’onde est mise en évidence sur le document 1 ? (spatiale ou temporelle). Justifier.

3. Mesurer le plus précisément la valeur de la longueur d’onde $\lambda$.

4. En déduire la célérité $\nu$ de l’onde dans les conditions de l’expérience.

Le document suivant représente les variations de l’élongation $y_0$ du point source $O$ en fonction du temps :

5. Vérifier que la valeur de la fréquence $f$ de vibration de la lame, déduite du document 2, est bien celle donnée par l’énoncé.

6. Les variations au cours du temps de l’élongation du point $B$, tel que $OB=75cm$, sont-elles en phase ou en opposition de phase avec le point $O$ source ? Justifier votre réponse.

7. Représenter en vert les variations au cours du temps de l’élongation du point $B$.

8. Calculer la tension $F$ (en $N$) de la corde dans les conditions de l’expérience.

Exercice 2 (6 pts)

Deux microphones $M_1$ et $M_2$ sont placés à proximité de l'axe perpendiculaire à la membrane de haut parleur et passant par son centre $O$ :

Le haut-parleur est branché à un générateur de tension sinusoïdale dont la fréquence et réglable.

Les microphones sont branchés à un oscilloscope dont les réglages figurent dans le tableau suivant :

Le document 2 est une reproduction de l'oscillogramme obtenu :

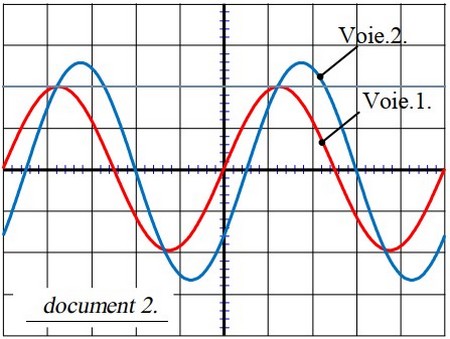
Dans les conditions de l'expérience, la célérité du son dans l'air est de l'ordre de $340m/s$.

1. Déterminer la période temporelle $T$ et la fréquence $f$ de l’onde sonore émise par le haut-parleur.

2. En déduire la période spatiale $\lambda$ de cette onde.

Ces courbes sont obtenues pour une distance minimale $d_{min}$ entre les deux microphones.

3. Déterminer le retard temporel entre les deux microphones.

4. En déduire la distance minimale $d_{min}$ séparant les deux microphones.

5. Pour quelles autres distances séparant les deux microphones obtiendrait-on le même oscillogramme.

On rapproche $M_2$ de $M_1$ d'une distance égale à $\frac{\lambda }{2}$.

6. Représenter l'oscillogramme obtenu.

Exercice 3 (7 pts)

Soit la transformation faisant réagir en milieu acide du peroxyde d'hydrogène ou "eau oxygénée" $H_2{O}_2$ et des ions iodure $I^{-}$.

Cette transformation peut être modélisée par la réaction d'équation :

$H_2{O}_{2 \left(aq\right)}+ 2I_{\left(aq\right)}^{-}+2H_3{O}_{\left(aq\right)}^{+}\to I_{2 \left(aq\right)}+4H_2{O}_{\left(l\right)}$

On désire, sachant que cette transformation est totale, en étudier la cinétique.

À la date $t=0s$, on ajoute une solution acidifiée d'iodure de potassium à une solution d’eau oxygénée de concentration telle que les ions iodure et les ions oxonium soient en excès.

À l’aide d’une technique adaptée, on obtient la courbe suivante donnant l’évolution temporelle de la concentration $\left[I_2\right]$ :

Les droites $\left({\Delta }_1\right)$ et $\left({\Delta }_2\right)$ sont les tangentes à la courbe respectivement en $t=0s$ et en $t=400s$.

Description du système chimique

1. Dresser le tableau d’avancement descriptif de la transformation chimique étudiée.

Aspect expérimental

2. En fonction du matériel présent dans la salle, proposer une des techniques de suivi cinétique de cette transformation chimique. Argumenter votre choix.

Étude cinétique

3. Pour chacune des espèces, préciser l’évolution de leur concentration au cours du temps.

4. Exprimer la vitesse de la réaction étudiée en fonction de la concentration  $\left[I_2\right]$.

5. Calculer la vitesse de réaction aux instants : $t=0s$ et $t=400s$.

6. A partir de la courbe, comparer les vitesses de réaction aux instants $t=0s$ et $t=400s$. Quel facteur cinétique permet d’expliquer ce résultat ?

7. Représenter l’allure de la courbe si on reproduit l’expérience à une température plus élevée. Justifier.