Séance 8 - Angles inscrits et angles au centre

Sommaire

I- Angle inscrit et angle au centre

1-1/ Angle au centre

1-2/ Angle inscrit

II- Deux angles inscrits interceptent le même arc de cercle

2-1/ Propriété

2-2/ Cas particulier

III- Relation entre l’angle au centre et l’angle inscrit qui interceptent le même arc de cercle

IV- Exercices

4-1/ Exercice 1

4-2/ Exercice 2

4-3/ Exercice 3

4-4/ Exercice 4

4-5/ Exercice 5

4-6/ Exercice 6

I- Angle inscrit et angle au centre

1-1/ Angle au centre

Définition

Dans un cercle, un angle au centre est un angle dont le sommet est le centre du cercle.

Exemple

On considère la figure suivante :

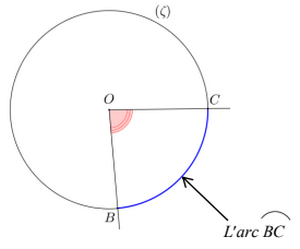
L’angle $\widehat{BOC}$ est appelé : angle au centre.

On dit que l’angle au centre BOC intercepte l’arc $\stackrel{⏜}{BC}$

I- Angle inscrit et angle au centre

1-2/ Angle inscrit

Définition

Dans un cercle, un angle inscrit est un angle dont le sommet est sur le cercle et dont les côtés coupent le cercle.

Exemple

On considère la figure suivante :

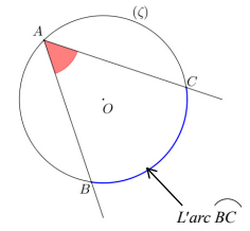
L’angle $\widehat{BAC}$ est appelé : angle inscrit.

On dit que l’angle inscrit $\widehat{BAC}$ intercepte l’arc $\stackrel{⏜}{BC}$

I- Angle inscrit et angle au centre

1-2/ Angle inscrit

Cas particulier d'angle inscrit

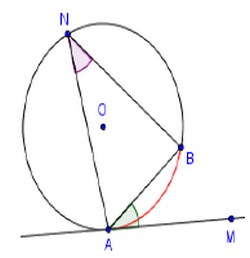
On considère la figure suivante telle (AC) est une tangente au cercle (C) en A :

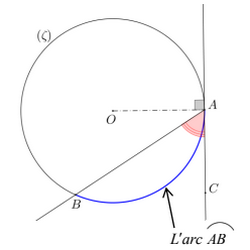
L’angle $\widehat{BAC}$ est appelé aussi angle inscrit. Il intercepte l’arc $\stackrel{⏜}{AB}$.

II- Deux angles inscrits interceptent le même arc de cercle

2-1/ Propriété

Dans un cercle, si deux angles inscrits interceptent le même arc de cercle (coupent le cercle aux mêmes points), alors ils ont la même mesure.

Exemple

Les angles inscrits $\widehat{BMA}$ et $\widehat{BNA}$ interceptent le même arc $\stackrel{⏜}{AB}$.

Alors : $\widehat{BMA}=\widehat{BNA}$

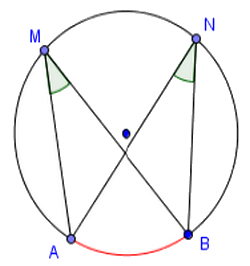
II- Deux angles inscrits interceptent le même arc de cercle

2-2/ Cas particulier

(AM) est la tangente au cercle en point A.

$\widehat{MAB}$ est appelé aussi un angle inscrit intercepte l’arc $\stackrel{⏜}{AB}$.

Donc : $\widehat{ANB}=\widehat{MAB}$.

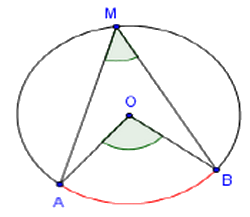
III- Relation entre l’angle au centre et l’angle inscrit qui interceptent le même arc de cercle

Propriété

Dans un cercle, si un angle inscrit et un angle au centre interceptent le même arc, alors la mesure de l’angle au centre est le double de celle de l’angle inscrit.

Exemple

L’angle au centre $\widehat{BOA}$ et l’angle inscrit $\widehat{BMA}$ interceptent le même arc $\stackrel{⏜}{AB}$.

Alors : $\widehat{BOA}=2\times \widehat{BMA}$

Ou : $\widehat{BMA}=\frac{1}{2}\times \widehat{BOA}$

IV- Exercices

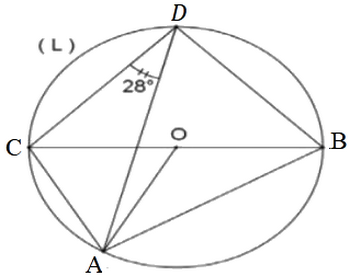
4-1/ Exercice 1

A et B et C et D sont 4 points qui appartiennent au périmètre du cercle (L) tel que : [CB] son diamètre et ADC=28°.

1. Déterminer avec justification les mesures des angles : $\widehat{ABC}$ ; $\widehat{AOC}$ ; $\widehat{BAC}$ et $\widehat{ACB}$.

IV- Exercices

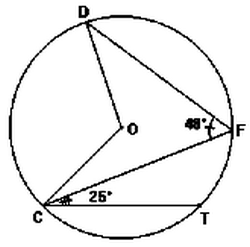
4-2/ Exercice 2

D’après la figure suivante $\widehat{DFC}=48°$ et $\widehat{FCT}=25°$

1)Calculer la mesure de l’angle $\widehat{FDT}$

2)Calculer la mesure de l’angle $\widehat{DTC}$

3)Calculer la mesure de l’angle $\widehat{DOC}$

IV- Exercices

4-3/ Exercice 3

(C) est un cercle circonscrit du tringle ABC de centre O.

1. Dessiner la figure

2. Prouver que : $\widehat{AOB}+\widehat{BOC}+\widehat{COA}=360°$

IV- Exercices

4-4/ Exercice 4

D’après la figure suivante, ABC est un triangle isocèle en A.

1. Prouver que [DA) est la bissectrice de l’angle $\widehat{BDC}$

IV- Exercices

4-5/ Exercice 5

Soit $I$ l'intersection des cordes $\left[AC\right]$ et $\left[BD\right]$ dans le cercle $\left(C\right)$ tels que $\widehat{IDC}=64°$ et $\widehat{DCI}=16°$ :

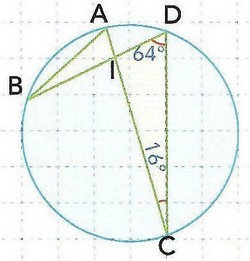
1. Déterminer les mesures des angles $\widehat{IAB}$ et $\widehat{IBA}$. (Justifier)

2. En déduire la mesure $\widehat{AIB}$.

IV- Exercices

4-6/ Exercice 6

Soit la figure suivante :

$\left[MC\right]$ et $\left[AH\right]$ se coupent en $B$.

1. Déterminer en justifiant la réponse la mesure de l'angle $\widehat{BMH}$.