Séance 7 - Triangle rectangle et trigonométrie

Sommaire

I- Cosinus, sinus et tangente d’un angle aigu

1-1/ Cosinus d’un angle aigu

1-2/ Sinus d’un angle aigu

1-3/ Tangente d’un angle aigu

1-4/ Propriété

II- Formules trigonométriques

2-1/ Propriété 1

2-2/ Propriété 2

2-3/ Angles particuliers

III- Exercices

3-1/ Exercice 1

3-2/ Exercice 2

3-3/ Exercice 3

3-4/ Exercice 4

3-5/ Exercice 5

3-6/ Exercice 6

I- Cosinus, sinus et tangente d’un angle aigu

1-1/ Cosinus d’un angle aigu

Définition

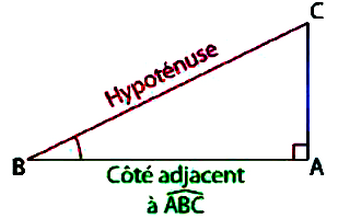
Dans un triangle rectangle, le cosinus d’un angle aigu est égal au quotient du côté adjacent sur l’hypoténuse.

Exemple

Dans un triangle ABC rectangle en A :

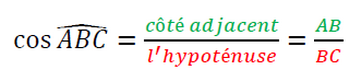
I- Cosinus, sinus et tangente d’un angle aigu

1-2/ Sinus d’un angle aigu

Définition

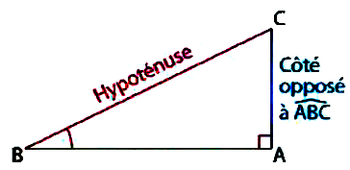
Le sinus d’un angle aigu est égal au quotient du côté opposé sur l’hypoténuse.

Exemple

Dans un triangle ABC rectangle en A :

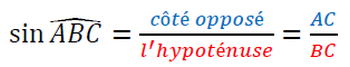
I- Cosinus, sinus et tangente d’un angle aigu

1-3/ Tangente d’un angle aigu

Définition

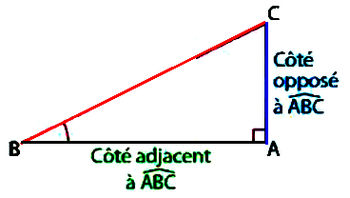
La tangente d’un angle aigu est égale au quotient du côté opposé sur le côté adjacent.

Exemple

Dans un triangle ABC rectangle en A :

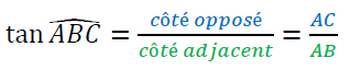
I- Cosinus, sinus et tangente d’un angle aigu

1-4/ Propriété

II- Formules trigonométriques

2-1/ Propriété 1

Pour tout angle aigu $\hat{a}$ on a :

$$\begin{gathered} \overline{) \\ {\cos }^2\hat{a}+{\sin }^2\hat{a}=1 \\ \tan \hat{a}=\frac{\sin \hat{a}}{\cos \hat{a}} \\ } \end{gathered}$$

II- Formules trigonométriques

2-2/ Propriété 2

Si $\hat{a}$ et $\hat{b}$ sont les mesures de deux angles complémentaires $\left(\hat{a}+\hat{b}\right)=90°$, alors :

$$\begin{gathered} \overline{) \\ \cos \hat{a}=\sin \hat{b} \\ \sin \hat{a}=\cos \hat{b} \\ \tan \hat{a}=\frac{1}{\tan \hat{b} } \\ } \end{gathered}$$

II- Formules trigonométriques

2-3/ Angles particuliers

III- Exercices

3-1/ Exercice 1

$ABC$ est un triangle tel que : $AB=\sqrt{3}$ et $AC=1$ et $BC=2$

1. Prouver que le triangle ABC est rectangle
2. Calculer $\cos \widehat{ABC}$, $\sin \widehat{ABC}$ et $\tan \widehat{ABC}$
3. Déduire la mesure de l’angle $\widehat{ABC}$

III- Exercices

3-2/ Exercice 2

$ABC$ est un triangle rectangle en $A$ tel que : $\sin \widehat{ABC}=\frac{3}{5}$ et $BC=15cm$

1. Calculer $\cos \widehat{ABC}$ et $\tan \widehat{ABC}$
2. Calculer $AB$ puis $AC$

III- Exercices

3-3/ Exercice 3

$\alpha$ est la mesure d’un angle aigu tel que : $0<\alpha <90°$
 
Simplifier :

$$\begin{gathered} \overline{) \\ A=\cos \alpha \left(\sin \alpha +\cos \alpha \right)-\sin \alpha \left(\cos \alpha -\sin \alpha \right)= \\ B=\frac{1}{1+\sin \alpha }+\frac{1}{1-\sin \alpha }-\frac{2}{{\cos }^2\alpha }= \\ C=\sin \alpha \times \sqrt{1-\cos \alpha }\times \sqrt{1+\cos \alpha }+{\cos }^2\alpha = \\ D=\sqrt{2}{\sin }^2\alpha +2\sin 45°{\cos }^2\alpha = \\ } \end{gathered}$$

III- Exercices

3-4/ Exercice 4

$\alpha$ est la mesure d’un angle non nul :

1. Calculer $\cos \alpha$ et $\tan \alpha$ sachant que $\sin \alpha =\frac{5}{7}$

2. Calculer $\sin \alpha$ et $\tan \alpha$ sachant que $\cos \alpha =\frac{4}{5}$

3. Calculer $\cos \alpha$ et $\sin \alpha$ sachant que $\tan \alpha =6$

III- Exercices

3-5/ Exercice 5

Calculer :

$$\begin{gathered} \overline{) \\ A=2\cos 15°+{\cos }^{2}36°-2\sin 75°+{\cos }^{2}54° \\ B={\cos }^{2}28°-{\sin }^{2}51°+{\cos }^{2}62°+{\cos }^{2}39° \\ C=\tan 73°\times \tan 17°-{\sin }^{2}40°-{\sin }^{2}50° \\ D={\sin }^{2}33°-4{\sin }^{2}30°+{\sin }^{2}57°+3\tan 50°\times \tan 40°= \\ } \end{gathered}$$

III- Exercices

3-6/ Exercice 6

a et b et c sont les mesures des angles d’un triangle.

Montrer que :

$$\begin{gathered} \overline{) \\ {\cos }^2\left(\frac{a+b}{2}\right)+{\cos }^2\left(\frac{c}{2}\right)=1 \\ } \end{gathered}$$