
Physique et Chimie : 2ème Année Bac
Séance 13 (Circuit RLC série en régime sinusoïdal forcé)
Professeur : Mr El GOUFIFA Jihad
Sommaire
I- Généralités sur le courant alternatif sinusoïdale
1-1/ L’intensité du courant électrique alternatif sinusoïdal
1-2/ La tension du courant électrique alternatif sinusoïdal
1-3/ Le déphasage
II- Étude d’un dipôle (RLC) série en régime sinusoïdal forcé
2-1/ Étude expérimentale
2-2/ Impédance d'un circuit RLC
III- Phénomène de résonance
3-1/ Étude expérimentale
3-2/ Grandeurs caractérisant la résonance
3-3/ Largeur de la bande passante à -3dB
3-4/ Facteur de qualité
IV- La puissance dans le régime sinusoïdal
4-1/ Puissance instantanée
4-2/ Puissance moyenne
V- Exercices
5-1/ Exercice 1
5-2/ Exercice 2
5-3/ Exercice 3
5-4/ Exercice 4
I- Généralités sur le courant alternatif sinusoïdale
1-1/ L’intensité du courant électrique alternatif sinusoïdal
L’intensité sinusoïdale s’écrit mathématiquement :
i(t)=Imcos(ωt+φ)
Où :
- Im : intensité maximale du courant électrique.
- ω=2πf : pulsation du courant électrique en (rad/s).
- φ : phase à l'origine (en rad)
L’intensité efficace I est reliée à l’intensité maximale par la relation :
I=Im√2
I- Généralités sur le courant alternatif sinusoïdale
1-2/ La tension du courant électrique alternatif sinusoïdal
La tension sinusoïdale s’écrit mathématiquement :
u(t)=Umcos(ωt+φ)
Où :
- Um : tension maximale du courant électrique.
- ω=2πf : pulsation du courant électrique en (rad/s).
- φ : phase à l'origine (en rad)
La tension efficace U est reliée à la tension maximale par la relation :
U=Um√2
Remarque
Les valeurs efficaces sont les valeurs indiquées par les instruments de mesure lorsqu'on les utilise en courant alternatif.
I- Généralités sur le courant alternatif sinusoïdale
1-3/ Le déphasage
On considère les fonctions suivantes :
i(t)=Imcos(ωt+φi)etu(t)=Umcos(ωt+φu)
On appelle le déphasage de u par rapport à i, la différence Δφ des deux signaux :
Δφ=φu-φi
On distingue les cas suivants :
- Si Δφ>0, alors on dit que u est en avance par rapport à i.
- Si Δφ<0, alors on dit que u est en retard par rapport à u.
- Si Δφ=0, alors on dit que u et i sont en phase.
- Si Δφ=π, alors on dit que u et i sont en opposition de phase.
- Si Δφ=π2, alors on dit que u et i en quadrature de phase.
II- Étude d’un dipôle (RLC) série en régime sinusoïdal forcé
2-1/ Étude expérimentale
On réalise le montage suivant :

On visualise sur l'écran de l'oscilloscope dans l'entrée Y2 la tension u(t) entre les bornes de RLC et dans l'entrée Y1 la tension uR(t) aux bornes du conducteur ohmique.
On obtient l'oscillogramme de la figure suivante :

On obtient des oscillations forcées car le générateur GBF impose sur circuit RLC sa fréquence et il l'oblige d'osciller avec cette fréquence, c'est le régime d'oscillations forcées.
Le générateur GBF s'appelle excitateur alors que le circuit RLC s'appelle résonateur.
II- Étude d’un dipôle (RLC) série en régime sinusoïdal forcé
2-2/ Impédance d'un circuit RLC
Généralement l’impédance est la résistance d’un circuit au passage d’un courant électrique alternatif sinusoïdale :
Z=UI=UmIm
Son unité est l’Ohm (Ω).
Les impédances de quelques composantes électriques :
- Un conducteur ohmique : Z=R
- Un condensateur : Z=1Cω
- Une bobine : Z=Lω
III- Phénomène de résonance
3-1/ Étude expérimentale
On réalise le montage suivant dans lequel la fréquence du générateur GBF est variable ainsi que la résistance r'.
L’inductance de la bobine est L=1,1H, et la capacité du condensateur est C=0,9μF.
On garde la tension efficace constante: U=2V
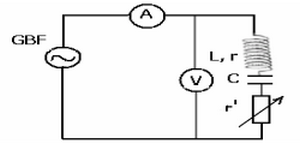
On mesure la variation de l'intensité efficace dans le circuit avec la variation de la fréquence puis on change la valeur de la résistance totale du circuit :
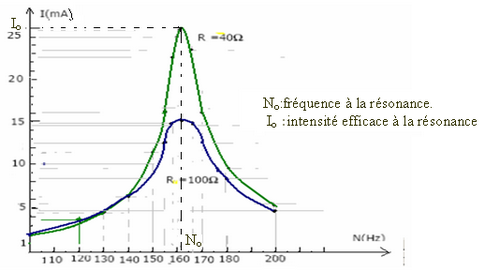
- À la résonance l'intensité efficace est maximale dans le circuit.
- Si la résistance du circuit est faible, la résonance est aiguë.
- Si la résistance du circuit est grande, la résonance est floue.
III- Phénomène de résonance
3-2/ Grandeurs caractérisant la résonance
Fréquence à la résonance
A la résonance la fréquence du générateur (excitateur) est égale à la fréquence propre du circuit :
III- Phénomène de résonance
3-2/ Grandeurs caractérisant la résonance
Fréquence à la résonance
Impédance du circuit à la résonance
A la résonance I est maximale donc l'impédance Z est minimale, elle égale à la résistance totale du circuit RLC
Donc à la résonance : .
On donne l'allure de la courbe qui représente la variation de Z en fonction de N :

III- Phénomène de résonance
3-2/ Grandeurs caractérisant la résonance
Intensité efficace du courant à la résonance
Déphasage à la résonance
u(t) et i(t) sont en phase, donc
III- Phénomène de résonance
3-3/ Largeur de la bande passante à -3dB
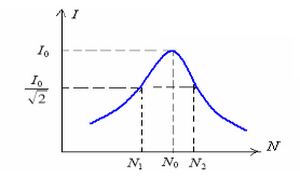
On appelle bande passante à -3 décibels d'un circuit RLC l'intervalle de fréquence du générateur pour lequel l'intensité efficace du courant est :
(: est l'intensité maximale efficace à la résonance)
La largeur de la bande passante est :
III- Phénomène de résonance
3-4/ Facteur de qualité
Le facteur de qualité d’un circuit (RLC) est donné par la relation :
C’est un facteur sans dimension caractérisant l’acuité de la résonance.
IV- La puissance dans le régime sinusoïdal
4-1/ Puissance instantanée
On considère un dipôle AB dans lequel passe un courant électrique et aux bornes duquel est appliquée une tension .
La puissance électrique instantanée est :
IV- La puissance dans le régime sinusoïdal
4-2/ Puissance moyenne
On considère un dipôle AB dans lequel passe un courant électrique et aux bornes duquel est appliquée une tension .
La puissance électrique moyenne est :
Avec est le facteur de puissance.
Remarque
La puissance moyenne se dissipe au niveau du circuit par effet Joule :
V- Exercices
5-1/ Exercice 1
Le circuit représenté sur la figure suivante contient :
- Un générateur GBF délivrant au circuit une tension sinusoïdale exprimée en et de fréquence réglable.
- Un conducteur ohmique de résistance .
- Une bobine (b) d’inductance et de résistance .
- Un condensateur de capacité .
- Un ampèremètre.
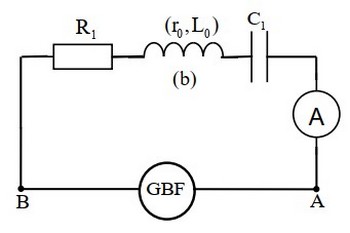
Le coefficient de qualité de ce circuit est , la largeur de la bande passante à est .
À la résonance, l’ampèremètre indique la valeur .
- Déterminer la fréquence des oscillations électriques à la résonance.
- Trouver la valeur de et celle de .
- Calculer la puissance électrique moyenne, consommée par effet joule, dans le circuit quand la fréquence prend l’une des valeurs limitant la bande passante.
V- Exercices
5-2/ Exercice 2
Un dipôle (R,L,C) série soumis à une tension excitatrice de fréquence variable, d’amplitude présente une résonance d’intensité de valeur à la fréquence .
- Quelle relation existe-t-il entre , et ?
- Calculer la valeur de la capacité connaissant l’inductance .
- Que vaut l’impédance du dipôle à la résonance ?
- Quelle caractéristique du circuit peut-on déduire ?
- Calculer le facteur de qualité du circuit. Ce dernier est -il sélectif ?
V- Exercices
5-3/ Exercice 3
On considère le montage électrique suivant, où le générateur applique aux bornes du dipôle une tension alternative sinusoïdale de la forme de tension maximale constante et de fréquence réglable :
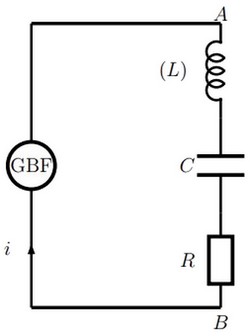
L’intensité instantanée dans le dipôle est noté .
On visualise au deux entrées de l’oscilloscope et les tensions et en utilisant la même sensibilité verticale des deux entrée et : et la sensibilité horizontale avec correspond à la tension et correspond la tension .
On fixe la fréquence à la valeur et la capacité du condensateur à la valeur .
La résistance du conducteur ohmique est .
On obtient l’oscillogramme suivant :

- Représenter sur le schéma les liaisons oscilloscope-circuit pour visualiser et .
- En utilisant l’oscillogramme, déterminer :
- (a) La période et la pulsation des oscillations.
- (b) La tension maximale et l’intensité maximale du courant .
- (c) le déphasage de la tension par rapport à l’intensité et écrire l’expression de .
À l’aide d’un voltmètre, on mesure la tension aux bornes de la bobine et après aux bornes du condensateur. On obtient successivement et .
- Calculer l’impédance du circuit.
- Calculer l’impédance aux bornes de la bobine, aux bornes du condensateur et aux bornes du conducteur ohmique. Quelle est votre conclusion ?
- Calculer les valeurs de l’inductance de la bobine et de la capacité du condensateur
- Calculer les deux grandeurs : et et les comparer et déduire la relation suivante :
V- Exercices
5-4/ Exercice 4
Un dipôle est constitué d’un condensateur de capacité , une bobine de résistance et d’induction et un conducteur ohmique de résistance .
Pour étudier le comportement de ce dipôle, on applique à l'aide d’un générateur de basse fréquence (GBF) entre ses bornes et une tension alternative sinusoïdale de valeur instantanée :
La valeur efficace de cette tension est maintenue constante et sa fréquence est réglable :

L'intensité instantanée du courant dans ce circuit est :
Une étude expérimentale a permis de suivre l’impédance du circuit en fonction de la fréquence . Les résultats obtenus ont abouti au diagramme suivant :
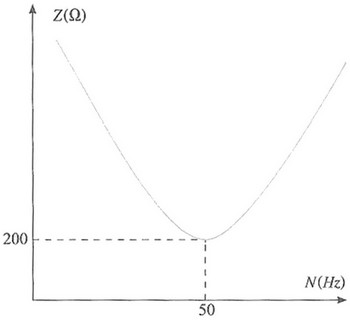
- Choisir les propositions correctes dans ce qui suit :
A- La grandeur qui, à la résonance, prend une valeur maximale est :
- l’intensité de courant.
- la tension .
- la puissance moyenne consommée par le dipôle .
B- La grandeur qui s’annule à la résonance est :
- l’impédance du circuit.
- le déphasage entre la tension et l’intensité .
C- Dans la zone passante de la résonance, l’intensité efficace du courant électrique vérifie la condition :
( : intensité efficace du courant à la résonance).
- Déterminer la résistance .
- Déterminer la capacité .
- Exprimer l’intensité lorsque la fréquence fixée sur .
Lorsqu’on fixe la fréquence sur la valeur , l’impédance du circuit prend le double de la valeur qu’elle prenait à la fréquence , et la puissance moyenne qu’il consomme représente de la puissance moyenne maximale.
- Déterminer numériquement l’intensité sachant qu’elle est en retard de phase sur la tension .


