
Physique et Chimie : 2ème Année Bac
Séance 12 (Les oscillations libres dans un circuit RLC série)
Professeur : Mr El GOUFIFA Jihad
Sommaire
I- Le circuit RLC
II- Décharge d’un condensateur dans une bobine
2-1/ Montage expérimentale
2-2/ Régimes d'amortissement
2-3/ Équation différentielle
III- Les oscillations non amorties dans un circuit idéal LC
3-1/ Le dipôle LC
3-2/ Montage expérimental
3-3/ Équation différentielle
3-4/ Solution de l’équation différentielle
3-5/ Expression de la période propre
3-6/ Expression de l'intensité du courant et de la change dans le circuit idéal LC
IV- Transfert d’énergie entre la bobine et le condensateur
4-1/ Expression de l'énergie totale d’un circuit LC
4-2/ Courbes de variation des énergies d'un circuit idéal LC
4-3/ Énergie du circuit RLC en série
V- Entretien des oscillations
VI- Exercices
6-1/ Exercice 1
6-2/ Exercice 2
6-3/ Exercice 3
6-4/ Exercice 4
I- Le circuit RLC
On appelle (RLC) l’association série d’un conducteur ohmique pur de résistance R, une bobine pure d’inductance L et d’un condensateur de capacité C.
Même si la bobine a une résistance interne r la nomination (RLC) reste valable.
II- Décharge d’un condensateur dans une bobine
2-1/ Montage expérimentale
On réalise le montage suivant :
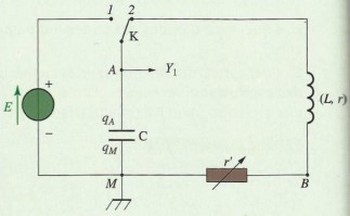
On place l'interrupteur K à la position (1) une durée suffisante pour que le condensateur soit chargé, puis on le bascule à la position 2 tout en visualisant à la voie Y1 sur l'écran d'un oscilloscope la tension aux bornes du condensateur.
On obtient ainsi un circuit RLC en série dans lequel la charge emmagasinée dans le condensateur oscille entre ses armatures car le condensateur se décharge et se charge régulièrement.
Mais grâce à l'existence de la résistance dans le circuit, la charge du condensateur diminue de même que la tension entre ses bornes : on dit que les oscillations sont amorties.
Et comme le circuit RLC ne comporte pas de générateur : les oscillations sont dites libres et amorties.
L'amortissement est due au fait qu'une partie de l'énergie électrique se perd sous forme de chaleur au niveau de la résistance du circuit par effet Joule.
II- Décharge d’un condensateur dans une bobine
2-2/ Régimes d'amortissement
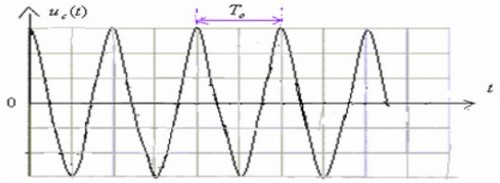
Le régime périodique
Si la résistance totale du circuit est nulle les oscillations sont libres et non amorties :
II- Décharge d’un condensateur dans une bobine
2-2/ Régimes d'amortissement
Le régime pseudopériodique
Si la résistance totale du circuit est faible les oscillations sont libres et amorties et leur amplitude diminue jusqu'à ce qu'il s'annule.
C'est l'état de l'amortissement faible.

II- Décharge d’un condensateur dans une bobine
2-2/ Régimes d'amortissement
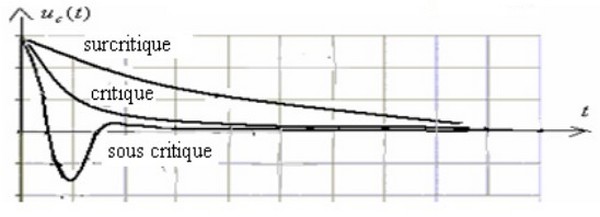
Le régime apériodique
Si la résistance totale du circuit est grande, les oscillations disparaissent car l'amortissement est fort, le condensateur perd sa charge sans oscillations et on distingue dans ce cas trois régimes :
- Le régime sous critique : la tension aux bornes du condensateur effectue une seule oscillation avant de s'annuler.
- Le régime critique : la tension aux bornes du condensateur s'annule sans oscillations.
- Le régime surcritique : la tension aux bornes du condensateur dure un temps très long pour s'annule sans oscillations.
II- Décharge d’un condensateur dans une bobine
2-3/ Équation différentielle
D’après la loi d’additivité des tensions, on a :
uL+uR+uC=0⇒Ldidt+Ri+qC=0⇒Ld2qdt2+Rdqdt+qC=0⇒LCd2uCdt2+RCduCdt+uC=0
C’est l’équation différentielle vérifiée par la tension uc entre les bornes du condensateur dans un circuit RLC en série.
Le terme résulte de l'amortissement (par son annulation l'amortissement disparaît).
II- Décharge d’un condensateur dans une bobine
2-3/ Équation différentielle
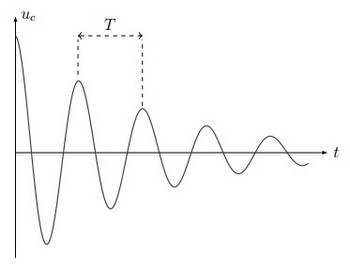
La pseudo-période
La pseudo-période est l’intervalle de temps qui sépare deux maximas consécutifs des oscillations pseudopériodiques amorties.
II- Décharge d’un condensateur dans une bobine
2-3/ Équation différentielle
Facteur de qualité d’un dipôle (RLC)
Un paramètre sans dimension soit noté Q, est appelé facteur de qualité du dipôle, il permet de séparer quantitativement les régimes d'amortissement.
Celui-ci peut s’exprimer en fonction des constantes de temps et des dipôles RL et RC déjà étudiés :
La résistance critique correspond à
La valeur de Q détermine les régimes libres d’un dipôle (RLC) :
- Q>0,5 : le régime est périodique amorti.
- Q=0,5 : le régime est critique.
- Q<0,5 : le régime est apériodique.
III- Les oscillations non amorties dans un circuit idéal LC
3-1/ Le dipôle LC
Le dipôle LC correspond au cas limite du dipôle RLC où la résistance est nulle : Les oscillations libres ne sont plus amorties.
On s’approche au mieux du régime oscillant non amorti en associant en série une bobine d’inductance L grande, de résistance r très petite et un condensateur de capacité C faible, afin d’avoir un grand facteur de qualité.
III- Les oscillations non amorties dans un circuit idéal LC
3-2/ Montage expérimental
On considère le montage expérimental suivant constitué d'un condensateur de capacité C initialement chargé et d'une bobine idéale d'inductance L et de résistance nulle r=0 (ce qui est difficile de réaliser pratiquement car quelque soit la bobine, sa
résistance est non nulle, donc c'est un circuit idéal) :
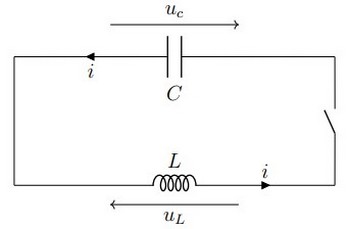
III- Les oscillations non amorties dans un circuit idéal LC
3-3/ Équation différentielle
D’après la loi d’additivité des tensions, on a :
C’est l’équation différentielle vérifiée par la tension uc entre les bornes du condensateur dans un circuit idéal LC.
III- Les oscillations non amorties dans un circuit idéal LC
3-4/ Solution de l’équation différentielle
C'est une fonction sinusoïdale de la forme :
- : tension aux bornes du condensateur en (V)
- : amplitude des oscillations (élongation maximale ) en (V)
- : phase du mouvement à l'instant t=0 en (rad).
- : période propre des oscillations en (s).
III- Les oscillations non amorties dans un circuit idéal LC
3-5/ Expression de la période propre
La solution de l'équation différentielle est :
Sa dérivée donne :
Sa dérivée seconde donne :
En remplaçant dans l'équation différentielle on obtient :
III- Les oscillations non amorties dans un circuit idéal LC
3-6/ Expression de l'intensité du courant et de la change dans le circuit idéal LC
L'expression de la charge du condensateur en fonction du temps est :
L'expression de l'intensité du courant :
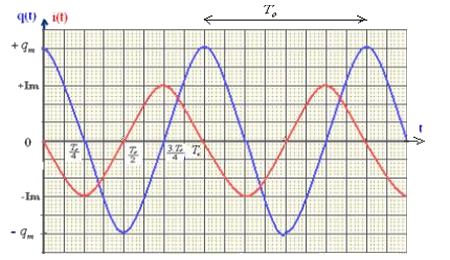
IV- Transfert d’énergie entre la bobine et le condensateur
4-1/ Expression de l'énergie totale d’un circuit LC
L'énergie totale d'un dipôle LC est la somme de l'énergie électrique emmagasinée dans le condensateur et de l'énergie magnétique emmagasinée dans la bobine.
Donc l'énergie totale du circuit LC est constante.
IV- Transfert d’énergie entre la bobine et le condensateur
4-2/ Courbes de variation des énergies d'un circuit idéal LC
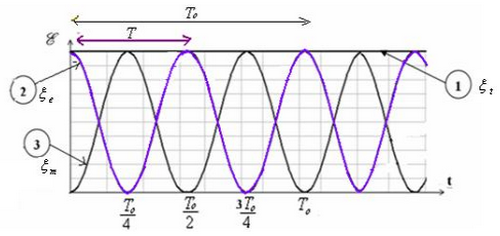
La période T de l'échange énergétique entre la bobine et le condensateur est égale à la moitié de la période propre .
Au cours des oscillations non amorties, l'énergie électrique emmagasinée dans le condensateur se transforme en énergie magnétique emmagasinée dans la bobine et inversement.
IV- Transfert d’énergie entre la bobine et le condensateur
4-3/ Énergie du circuit RLC en série
L'énergie totale d'un dipôle RLC est :
En appliquant la loi d 'additivité des tensions on a :
D'autre part on a :
Donc l'énergie totale du circuit RLC est décroissante.
L'énergie totale du circuit RLC décroît en fonction du temps et les oscillations sont amorties à cause de la perte de l'énergie électrique par effet joule au niveau de la résistance.
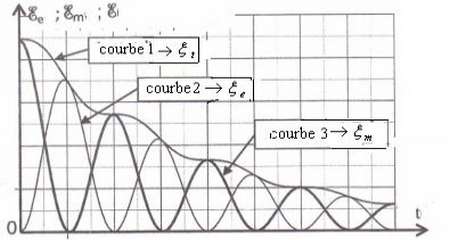
V- Entretien des oscillations
Pour entretenir les oscillations on doit utiliser un générateur d’entretien pour récompenser l'énergie perdue par effet Joule à chaque oscillation.
 |
Si , cad la tension au borne du générateur est proportionnelle à l’intensité de courant et que le coefficient de proportionnalité est (R+r), alors
VI- Exercices
6-1/ Exercice 1
On considère le montage de la figure suivante :

On charge le condensateur de capacité à l'aide d'un générateur de force électromotrice puis on bascule l'interrupteur à la position (2) en prenant cet instant comme origine des temps.
On donne : , : inductance de la bobine est variable, .
Lorsque le condensateur est totalement chargé, on bascule l'interrupteur à la position (2) à un instant .
La courbe de la figure suivante donne l'évolution temporelle de la charge du condensateur :
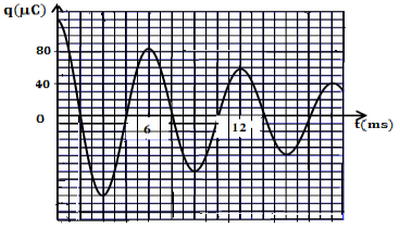
- Nommer le régime oscillatoire correspondant.
- En considérant que la pseudo-période est égale à la période propre, déterminer la valeur de l'inductance (On prend ).
- Calculer la variation de l'énergie totale du circuit entre les instants et . Interpréter le résultat obtenue.
Pour entretenir les oscillations, on monte en série avec le condensateur et la bobine précédente un générateur qui délivre une tension électrique .
- Établir l'équation différentielle vérifiée par la charge .
Lorsque la constante prend la valeur , on obtient des oscillations électriques sinusoïdales.
- En déduire la valeur de la résistance de la bobine.
VI- Exercices
6-2/ Exercice 2
On réalise le montage représenté dans la suivante qui comprend en série :
|
 |
On ferme l'interrupteur à .
La figure 2 représente les variations de la tension uc aux bornes du condensateur :

- Montrer que l'équation différentielle vérifiée par s'écrit ( une constante à exprimer) :
La solution de l'équation différentielle s'écrit sous la forme :
- Exprimer la tension aux bornes du condensateur à en fonction de , et . Calculer sa valeur.
- Montrer que ou est un entier naturel non nul.
- Déduire que .
- En déduire l’énergie dissipée par effet joule au bout des trois premières pseudo-périodes.
VI- Exercices
6-3/ Exercice 3
On charge un condensateur de capacité C à l'aide d'un générateur de force électromotrice E, puis on bascule l'interrupteur K à la position (2) en prenant cet instant comme origine des temps :
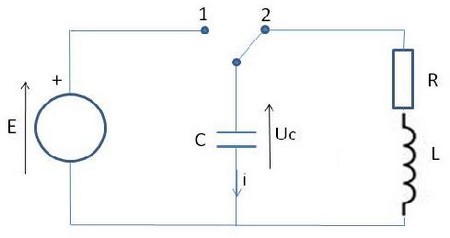
On donne : , L : inductance de la bobine est variable (sa résistance est négligeable), et .
La tension aux bornes du condensateur évolue en fonction du temps comme le montre la figure suivante :

- Les oscillations électriques observées sont amorties. Quel est le dipôle responsable de cet amortissement ?
- Qualifier ce régime d'oscillations par un terme approprié.
- Sur la courbe de la figure précédente sont indiqués deux points A et B. Comment appelle-t-on la durée entre ces deux points ? Déterminer graphiquement sa valeur.
- Établir l'équation différentielle vérifiée par la tension aux bornes du condensateur.
Pour entretenir les oscillions on ajoute dans le circuit précédent un dispositif.
- Expliquer dans une phrase, le rôle de ce dispositif du point de vue énergétique.
- Donner l'expression de la période propre du circuit oscillant et calculer sa valeur .On donne : et .
- En déduire la fréquence de la tension obtenue.
Le circuit oscillant est ensuite relié à un haut parleur convertissant cette onde électrique en une onde sonore de fréquence .
On souhaite que notre instrument émet la note à l'aide du circuit précédent.
On donne les fréquences de l'octave 3 de la gamme tempérée:
| Note | do | Ré | mi | fa | sol | si | |
| Fréquence (en Hz) | 262 | 294 | 330 | 349 | 392 | 440 | 494 |
- La fréquence précédente obtenue est-elle un son de l'octave 3 de la gamme ?
- Quels paramètre peut-on changer pour modifier la valeur de la fréquence émise ?
- Sachant qu'on ne dispose pas d'autres condensateurs que celui du circuit précédent, calculer la valeur de l'autre paramètre qui permettra d'obtenir la note .
On règle ce paramètre sur .
- Déterminer la nature de la note émise par le diapason.
VI- Exercices
6-4/ Exercice 4
On considère le montage suivant qui se compose d'un générateur de force électromotrice, d'un condensateur de capacité , d'une bobine de coefficient d'induction et de résistance négligeable et d'un conducteur ohmique de résistance variable :

On ferme l'interrupteur à la position (1) à l'instant .
- Établir l'équation différentielle vérifiée par la tension aux bornes du condensateur. (On pose ).
- Montrer que est solution de l'équation différentielle précédente puis déduire l'expression de et de .
- En utilisant l'analyse dimensionnelle déterminer l'unité de .
- Montrer que l'énergie électrique maximale emmagasinée dans le condensateur est .
- Montrer que l'énergie électrique emmagasinée dans le condensateur est .
On donne dans la figure suivante la courbe qui représente les variations de l'énergie électrique emmagasinée dans le condensateur en fonction du temps :
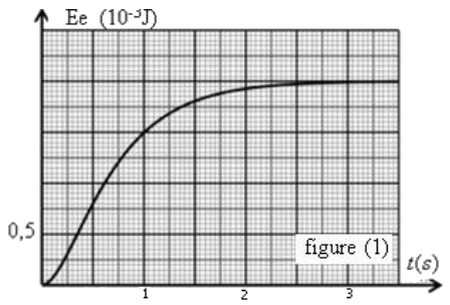
- Déterminer graphiquement la valeur de .
- Déduire la valeur de la capacité du condensateur sachant que la force électromotrice du générateur est .
- Montrer que .
Lorsque le régime permanent est établit on décale l'interrupteur vers la position (2) à un instant .
On obtient La courbe (1) qui représente les variations de la tension uc aux bornes du condensateur en fonction du temps :
- Nommer le régime que représente chacune des courbes.
- Déterminer la charge du condensateur à l'instant .
On fait diminuer la valeur de la résistance et on obtient la courbe (2).
- Déterminer graphiquement la valeur de la pseudo-période de l'oscillateur.
- Sachant que la pseudo-période est égale à la période propre, déterminer la valeur du coefficient d'induction de la bobine (On prend ).
- Monter que l'énergie totale du circuit diminue. Interpréter cette diminution.
Lorsque le condensateur est totalement chargé, on fait varier la valeur de la résistance jusqu'à ce qu'elle s'annule (), puis on décale l'interrupteur vers la position (2) à un instant .
- Déterminer l'équation différentielle vérifiée par la tension aux bornes du condensateur.
- Montrer que est solution de l'équation différentielle précédente, puis déterminer l'expression de en fonction des paramètres du circuit et déterminer sa valeur.


