Séance 6 - Triangles et droites parallèles

Sommaire

I- La droite qui passe par les milieux de deux côtés d'un triangle

II- La distance entre les milieux de deux côtés d'un triangle

III- La droite qui passe par le milieu d'un côté d'un triangle et parallèle au deuxième côté

IV- La droite qui coupe deux côtés d'un triangle et parallèle au troisième côté

V- Exercices

5-1/ Exercice 1

5-2/ Exercice 2

5-3/ Exercice 3

5-4/ Exercice 4

5-5/ Exercice 5

5-6/ Exercice 6

5-7/ Exercice 7

I- La droite qui passe par les milieux de deux côtés d'un triangle

1-1/ Propriété 1

La droite qui passe par les milieux de deux côtes d’un triangle est parallèle au troisième côté.

Autrement dit

Exemple

I- La droite qui passe par les milieux de deux côtés d'un triangle

1-2/ Remarques importantes

Pour appliquer cette propriété en a besoin d’un triangle et les milieux de deux côtés.

On utilise cette propriété pour montrer que deux droites sont parallèles.

II- La distance entre les milieux de deux côtés d'un triangle

2-1/ Propriété 2

La distance entre les milieux de deux côtes d’un triangle est égale à la moitié de la longueur du troisième côté.

Autrement dit

Exemple

II- La distance entre les milieux de deux côtés d'un triangle

2-2/ Remarques importantes

Pour appliquer cette propriété en a besoin d’un triangle et les milieux de deux côtés.

On utilise cette propriété pour calculer les longueurs.

III- La droite qui passe par le milieu d'un côté d'un triangle et parallèle au deuxième côté

3-1/ Propriété 3

La droite qui passe par le milieu du côté d’un triangle et parallèle au deuxième côté coupe le troisième côté en son milieu.

Autrement dit

Exemple

III- La droite qui passe par le milieu d'un côté d'un triangle et parallèle au deuxième côté

3-2/ Remarques importantes

Pour appliquer cette propriété en a besoin d’un triangle, le milieu d’un côté et d’une Parallèle au deuxième côté qui passe par ce milieu.

On utilise cette propriété pour montrer le milieu du côté d’un triangle.

IV- La droite qui coupe deux côtés d'un triangle et parallèle au troisième côté

4-1/ Propriété 4

Exemple

IV- La droite qui coupe deux côtés d'un triangle et parallèle au troisième côté

4-2/ Remarques importantes

Pour appliquer cette propriété en a besoin d’un triangle, de deux points qui appartiennent à deux côté et d’une parallèle au troisième côté qui passe par ces deux points.

On utilise cette propriété pour calculer les longueurs.

V- Exercices

5-1/ Exercice 1

Sur la figure suivante, on a AB=8cm et BC=6cm :

1. Démontrer que les droites (IJ) et (BC) sont parallèles et calculer la longueur IJ.
2. Démontrer que les droites (LK ) et (AB) sont parallèles et calculer la longueur LK.

V- Exercices

5-2/ Exercice 2

ABCD est un parallélogramme de centre O

I est le milieu de [AD] et J est le milieu de [CD].

1. Montrer que (IJ) et (AC) sont parallèles.

La droite (BD) coupe (IJ) en E.

2. Montrer que E est le milieu de [OD].

V- Exercices

5-3/ Exercice 3

1. Reproduire la figure ci-dessous en vraie grandeur.

Soit J le milieu de [AC] et I le milieu de [AB].

2. Démontrer que les droites (JI) et (CB) sont parallèles (considérer le triangle ABC).

La parallèle à (BD) passant par I coupe (AD) en K.

3. Démontrer que K est le milieu de [AD] (considérer triangle ABD).

4. Calculer IJ et JK en justifiant (considérer ABC puis ABD).

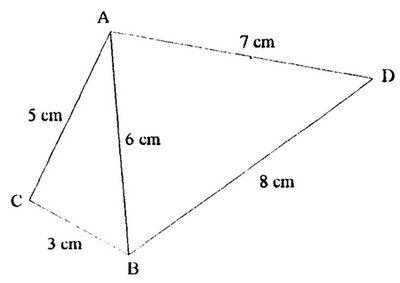
V- Exercices

5-4/ Exercice 4

T et S sont des points des cotes [MN] et [MO] du triangle MNO  tel que : (TS) // (NO) et TS=x et SO=y

1. Calculer x
2. Calculer y

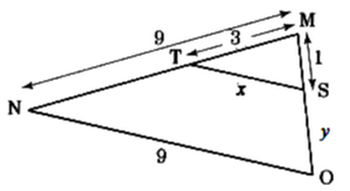
V- Exercices

5-5/ Exercice 5

ABCD est un trapèze de bases [AB] et [CD] tel que : AB=4cm et CD=6cm

I est le milieu de [AD] et J est le milieu de [BD]

1. Construire la figure

2. Montrer que (IJ) // (AB)

3. En déduire que (IJ) // (CD)

4. Calculer IJ

La droite (IJ) coupe (BC) en K

5. Montrer que K est le milieu de [BC]

6. Montrer que: AB+CD=2IK

V- Exercices

5-6/ Exercice 6

$ABCD$ un parallélogramme de centre $O$ tel que $AB=6cm$ et $BC=4cm$.

Soit $I$ le milieu de $\left[BC\right]$.

1. Faire une figure.

2. Montrer que : $\left(OI\right)//\left(AB\right)$

3. Montrer que : $OI=3cm$

La parallèle à $\left(BD\right)$ qui passe par $I$ coupe $\left(DC\right)$ en $J$.

4. Montrer que : $OB=IJ$

V- Exercices

5-7/ Exercice 7

Soit la figure suivante :

$I$ est le milieu de $\left[EF\right]$, $J$ est le milieu de $\left[FG\right]$ et $EG=5cm$.

1. Montrer que : $\left(IJ\right)//\left(EG\right)$

2. Déterminer, en justifiant la réponse, la longueur des segments $\left[IJ\right]$.

La parallèle à $\left(FH\right)$ passant par $I$ coupe le segment $\left[EH\right]$ en $O$.

3. Que représente $O$ pour $\left[EH\right]$ ? Justifier.