Séance 4 - Théorème de Thalès

Sommaire

I- Le théorème de Thalès direct

1-1/ Énoncé du théorème

1-2/ Configurations de Thalès

1-3/ Utilisation de Thalès

II- La réciproque du théorème de Thalès

2-1/ Énoncé du théorème

2-2/ Utilisation du réciproque de Thalès

III- Exercices

3-1/ Exercice 1

3-2/ Exercice 2

3-3/ Exercice 3

3-4/ Exercice 4

3-5/ Exercice 5

3-6/ Exercice 6

3-7/ Exercice 7

I- Le théorème de Thalès direct

1-1/ Énoncé du théorème

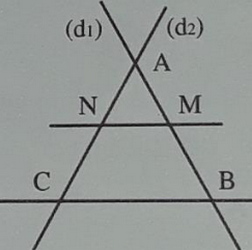
Soient deux droites (d) et (d′) sécantes en A.

• B et M sont deux points de (d) distincts de A.
• C et N sont deux points de (d’) distincts de A.

Si les droites (BC) et (MN) sont parallèles, alors :

$\overline{) \frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC} }$

I- Le théorème de Thalès direct

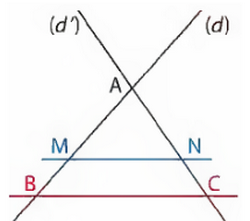
1-2/ Configurations de Thalès

I- Le théorème de Thalès direct

1-3/ Utilisation de Thalès

On utilise le Théorème de Thalès pour calculer les longueurs et comparer ou calculer des rapports de longueurs.

Exemple

Dans la figure ci-dessous on a $\left(d\right)$ et $(d\text{'})$ deux droites sécantes en A avec :

• $M\in \left(AB\right)$ et $N\in \left(AC\right)$ et $\left(MN\right)\parallel \left(BC\right)$
• $AM=20$ et $AN=25$ et $AC=45$ et $BC=27$

On calcule AB et MN

II- La réciproque du théorème de Thalès

2-1/ Énoncé du théorème

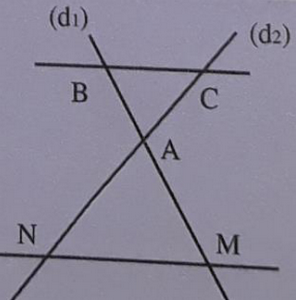
Soient (d) et (d') deux droites sécantes en A.

• B et M sont deux points de (d) distincts de A.
• C et N sont deux points de (d;) distincts de A.

Si les points A, B, M et les points A, C, N sont alignés dans le même ordre, et si: $\frac{AM}{AB}=\frac{AN}{AC}$, alors les droites (BC) et (MN) sont parallèles.

II- La réciproque du théorème de Thalès

2-2/ Utilisation du réciproque de Thalès

La réciproque du théorème de Thalès permet de démontrer le parallélisme de deux droites.

Attention, il ne suffit pas de vérifier l’égalité des rapports : il faut aussi s’assurer que les points sont bien placés dans le même ordre.

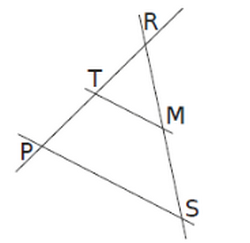
Exemple

Sur la figure ci-dessous on a : RT = 6, RP = 8, RM = 4,5 et RS = 6.

On veut montrer que les droites (MT) et (SP) sont parallèles.

III- Exercices

3-1/ Exercice 1

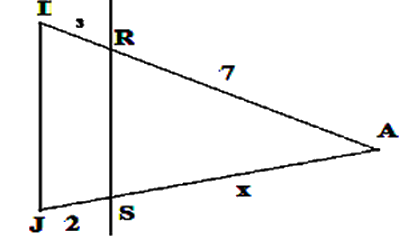
Dans la figure suivante : $\left(RS\right) // \left(IJ\right)$

IR=3 et AR=7 et AS=x et JS=2

• Calculer x

III- Exercices

3-2/ Exercice 2

Dans la figure suivante : $\left(BC\right) // \left(DE\right)$

AC=y et AB=7 et AE=x et AD=8 et BC=6 et DE=9

• Calculer x et y

III- Exercices

3-3/ Exercice 3

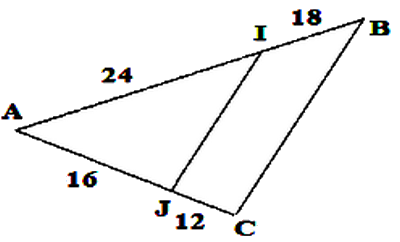
Dans la figure suivante :

AJ=16 et AI=24 et JC=12 et IB=18

• Montrer que : $\left(BC\right) // \left(IJ\right)$

III- Exercices

3-4/ Exercice 4

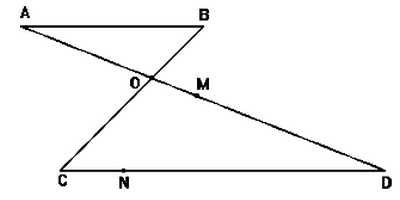
Dans la figure suivante : $\left(AB\right) // \left(CD\right)$

AB=3 et OC=5 et DC=10 et OD=8

1. Calculer les longueurs : OA et OB

On pose : DM=6,4 et DN=8

2. Montrer que $\left(OC\right) // \left(MN\right)$

III- Exercices

3-5/ Exercice 5

Dans la figure suivante (CE) et (BD) deux droites sécantes en point A, tel que :

BD=6 et AB=12 et AC=10 et CE=5

1. Calculer $\frac{AD}{AB}$ et $\frac{AE}{AC}$

2. Déduire que $\left(DE\right) // \left(BC\right)$

III- Exercices

3-6/ Exercice 6

Soit ABC un triangle dans lequel on a tracé une droite (ED) tel que $\left(ED\right) // \left(BC\right)$.

On donne AE=BC=3 et EB=AD=2.

1. Calculer AC, puis DC.

2. Calculer ED.

F est un point de (DE) tel que DF=2,7

3. Les droites (EC) et (AF) sont-elles parallèles ?

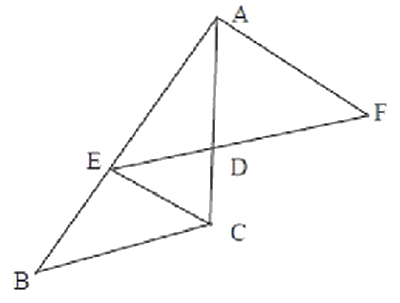
III- Exercices

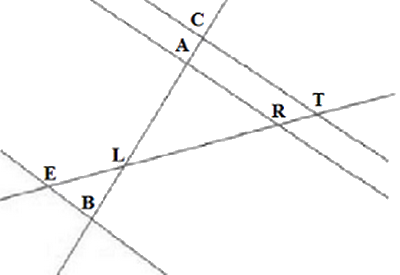
3-7/ Exercice 7

Sur la figure ci-dessous, (AR) // (CT).

Les points E, L, R et T sont alignés.

Les points C, A, L et B sont alignés.

On donne LC = 6 et LT = 9 et LA = 4,8 et LB = 1,5 et LE = 3.

1. Calculer LR.

2. Les droites (EB) et (CT) sont-elles parallèles ?