Séance 3 - Racines carrées

Sommaire

I- La racine carrée d’un nombre réel positif

1-1/ Définition

1-2/ Propriété (Le carré d’une racine carrée)

1-3/ Remarques importantes

II- Résolution de l’équation $x^2=a$

2-1/ $a>0$

2-2/ $a=0$

2-3/ $a<0$

III- Les opérations sur les racines carrées

3-1/ Produit de deux racines carrées

3-2/ Quotient de deux racines carrées

3-3/ Rendre un dénominateur rationnel ou supprimer le radical au dénominateur

IV- Exercices

4-1/ Exercice 1

4-2/ Exercice 2

4-3/ Exercice 3

4-4/ Exercice 4

4-5/ Exercice 5

4-6/ Exercice 6

I- La racine carrée d’un nombre réel positif

1-1/ Définition

Soit $a$ un nombre réel positif ou nul ( c'est-a-dire $a\ge 0$).

La racine carrée de $a$ est le nombre réel positif dont le carré est égale à $a$, elle est notée $\sqrt{a}$.

Le symbole s'appelle : symbole radical.

1-2/ Propriété (Le carré d’une racine carrée)

Soit a un nombre réel tel que a> 0.

$\sqrt{a^2}={\left(\sqrt{a}\right)}^2=a et \sqrt{{\left(-a\right)}^2}=a$

Exemple

I- La racine carrée d’un nombre réel positif

1-3/ Remarques importantes

La racine carrée d’un nombre négatif n’existe pas ($\sqrt{-9}$ n’existe pas) .

La racine carrée d’un nombre n’est jamais égale à un nombre négatif $\left(\sqrt{25}\ne -5\right)$.

L’opposé de $\sqrt{a}$ (avec $a\ge 0$) est $-\sqrt{a}$ . (L’opposé de $\sqrt{11}$ est $-\sqrt{11}$) .

$\sqrt{0}=0$ et $\sqrt{1}=1$

1-4/ Les racines carrées parfaites

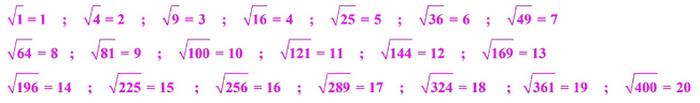
II- Résolution de l’équation $x^2=a$

2-1/ $a>0$

L’équation $x^2=a$ est respectivement équivalente à :

$$\begin{gathered} \overline{){\mathrm{x}}^{\mathrm{2}}\mathrm{-}\mathrm{a}\mathrm{=}\mathrm{0} \\ \mathrm{\Rightarrow }{\mathrm{x}}^{\mathrm{2}}\mathrm{-}{\sqrt{\mathrm{a}}}^{\mathrm{2}}\mathrm{=}\mathrm{0} \\ \mathrm{\Rightarrow }(x-\sqrt{a})(x+\sqrt{a})\mathrm{=}\mathrm{0} \\ \mathrm{\Rightarrow }(x-\sqrt{a})\mathrm{=}\mathrm{0}\mathrm{ }\mathrm{o}\mathrm{u}\mathrm{ }(x+\sqrt{a})\mathrm{=}\mathrm{0} \\ \mathrm{\Rightarrow }\mathrm{x}\mathrm{=}\sqrt{\mathrm{a}}\mathrm{ }\mathrm{o}\mathrm{u}\mathrm{ }\mathrm{x}\mathrm{=}\mathrm{-}\sqrt{\mathrm{a}} \\ } \end{gathered}$$

Donc cette équation admet deux solutions: $\sqrt{a}$  et $-\sqrt{a}$.

2-2/ $a=0$

L’équation $x^2=a$ est respectivement équivalente à :$x^2=0$ , ce qui signifie que $x=0$.

Donc cette équation admet pour solution le nombre 0.

2-3/ $a<0$

L’équation $x^2=a$ n’admet pas de solution.

III- Les opérations sur les racines carrées

3-1/ Produit de deux racines carrées

Propriété

Soient a et b deux nombres réels positifs.

$\overline{)\mathrm{ }\sqrt{\mathrm{a}}\mathrm{\times }\sqrt{\mathrm{b}}\mathrm{=}\sqrt{\mathrm{a}\mathrm{\times }\mathrm{b}}\mathrm{ }}$

Exemple

Extraire un carré parfait

Soient a et b deux nombres réels positifs non nuls.

$\overline{)\mathrm{ }\sqrt{{\mathrm{a}}^{\mathrm{2}}\mathrm{\times }\mathrm{b}}\mathrm{=}\mathrm{a}\sqrt{\mathrm{b}}\mathrm{ }}$

Exemple

III- Les opérations sur les racines carrées

3-2/ Quotient de deux racines carrées

Propriété

Soient a et b deux nombres réels tels que $a\ge 0$ et $b>0$.

$\overline{)\mathrm{ }\frac{\sqrt{\mathrm{a}}}{\sqrt{\mathrm{b}}}\mathrm{=}\sqrt{\frac{\mathrm{a}}{\mathrm{b}}}\mathrm{ }}$

Exemple

III- Les opérations sur les racines carrées

3-3/ Rendre un dénominateur rationnel ou supprimer le radical au dénominateur

Propriété  1

Soient a et b et k deux nombres réels tels que b> 0.

$\overline{)\mathrm{ }\sqrt{\frac{\mathrm{1}}{\mathrm{b}}}\mathrm{=}\frac{\mathrm{1}}{\sqrt{\mathrm{b}}}\mathrm{ }\mathrm{=}\frac{\sqrt{\mathrm{b}}}{\mathrm{b}}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{ }\frac{\mathrm{a}}{\sqrt{\mathrm{b}}}\mathrm{=}\frac{\mathrm{a}\sqrt{\mathrm{b}}}{\mathrm{b}}\mathrm{ }\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{ }\frac{\mathrm{a}}{\mathrm{k}\sqrt{\mathrm{b}}}\mathrm{=}\frac{\mathrm{a}\sqrt{\mathrm{b}}}{\mathrm{k}\mathrm{b}}\mathrm{ }}$

Exemple

Propriété 2 (Expression du conjugué)

Pour supprimer le radical au dénominateur, on multiplie le numérateur et le dénominateur par le conjugué du dénominateur.

Le conjugué de a- b est a+b, et le conjugué de a+b est a- b.

Exemple

IV- Exercices

4-1/ Exercice 1

Calculer:

IV- Exercices

4-2/ Exercice 2

Simplifier sous la forme de $a\sqrt{b}$ tel que $a$ et $b$ sont des nombres réels et $b\ge 0$ :

$$\begin{gathered} \overline{) \\ \mathrm{ }\mathrm{A}\mathrm{=}\mathrm{-}\mathrm{3}\sqrt{\mathrm{2}}\mathrm{+}\mathrm{5}\sqrt{\mathrm{2}}\mathrm{-}\mathrm{2}\sqrt{\mathrm{2}}\mathrm{=}\mathrm{ }\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{ } \\ \mathrm{ }\mathrm{B}\mathrm{=}\mathrm{-}\mathrm{2}\sqrt{\mathrm{3}}\mathrm{+}\sqrt{\mathrm{3}}\mathrm{-}\mathrm{5}\sqrt{\mathrm{3}}\mathrm{+}\mathrm{4}\sqrt{\mathrm{3}}\mathrm{=}\mathrm{ }\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{ } \\ \mathrm{ }\mathrm{C}\mathrm{=}\mathrm{2}\sqrt{\mathrm{5}}\mathrm{+}\mathrm{3}\sqrt{\mathrm{5}}\mathrm{-}\mathrm{9}\sqrt{\mathrm{5}}\mathrm{+}\sqrt{\mathrm{5}}\mathrm{=}\mathrm{ }\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{ } \\ \mathrm{ }\mathrm{D}\mathrm{=}\mathrm{\left(}\sqrt{\sqrt{\mathrm{5}}\mathrm{-}\mathrm{2}}\mathrm{\right)}\mathrm{\times }\mathrm{\left(}\sqrt{\sqrt{\mathrm{5}}\mathrm{+}\mathrm{2}}\mathrm{\right)}\mathrm{=}\mathrm{ }\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{ } \\ \mathrm{ }\mathrm{E}\mathrm{=}\mathrm{\left(}\sqrt{\mathrm{2}\sqrt{\mathrm{7}}\mathrm{-}\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{\right)}\mathrm{\times }\mathrm{\left(}\sqrt{\mathrm{2}\sqrt{\mathrm{7}}\mathrm{+}\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{\right)}\mathrm{=}\mathrm{ }\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{ } \\ } \end{gathered}$$

IV- Exercices

4-3/ Exercice 3

1. Simplifier sous la forme de $a\sqrt{b}$ tel que $a$ et $b$ sont des nombres réels et $b\ge 0$ :

$$\begin{gathered} \overline{) \\ \mathrm{ }\mathrm{A}\mathrm{=}\sqrt{\mathrm{80}}\mathrm{+}\mathrm{3}\sqrt{\mathrm{125}}\mathrm{-}\sqrt{\mathrm{45}}\mathrm{=}\mathrm{ }\mathrm{\_\_\_\_\_\_\_\_\_}\mathrm{ } \\ \mathrm{ }\mathrm{B}\mathrm{=}\mathrm{2}\sqrt{\mathrm{18}}\mathrm{-}\mathrm{5}\sqrt{\mathrm{8}}\mathrm{+}\sqrt{\mathrm{200}}\mathrm{=}\mathrm{ }\mathrm{\_\_\_\_\_\_\_\_\_}\mathrm{ } \\ \mathrm{ }\mathrm{C}\mathrm{=}\sqrt{\mathrm{99}}\mathrm{-}\sqrt{\mathrm{176}}\mathrm{+}\mathrm{2}\sqrt{\mathrm{44}}\mathrm{=}\mathrm{ }\mathrm{\_\_\_\_\_\_\_\_\_}\mathrm{ } \\ \mathrm{ }\mathrm{D}\mathrm{=}\mathrm{-}\sqrt{\mathrm{27}}\mathrm{+}\sqrt{\mathrm{75}}\mathrm{-}\mathrm{4}\sqrt{\mathrm{48}}\mathrm{=}\mathrm{ }\mathrm{\_\_\_\_\_\_\_\_\_}\mathrm{ }\mathrm{ } \\ } \end{gathered}$$

2. Calculer :

$$\begin{gathered} \overline{) \\ \mathrm{ }\mathrm{E}\mathrm{=}\sqrt{\mathrm{150}}\mathrm{\times }\sqrt{\frac{\mathrm{3}}{\mathrm{162}}}\mathrm{=}\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ } \\ \mathrm{ }\mathrm{F}\mathrm{=}\mathrm{ }\sqrt{\frac{\mathrm{3}}{\mathrm{10}}}\mathrm{\times }\sqrt{\frac{\mathrm{270}}{\mathrm{8}}}\mathrm{=}\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ } \\ \mathrm{ }\mathrm{G}\mathrm{=}\sqrt{\frac{\mathrm{8}}{\mathrm{27}}}\mathrm{\times }\sqrt{\frac{\mathrm{3}}{\mathrm{50}}}\mathrm{=}\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ } \\ } \end{gathered}$$

IV- Exercices

4-4/ Exercice 4

Résoudre les équations suivantes :

$$\begin{gathered} \overline{) \\ \mathrm{ }{\mathrm{x}}^{\mathrm{2}}\mathrm{=}\mathrm{16} \\ \mathrm{ }{\mathrm{x}}^{\mathrm{2}}\mathrm{=}\mathrm{-}\mathrm{4} \\ \mathrm{ }\mathrm{-}\mathrm{5}{\mathrm{x}}^{\mathrm{2}}\mathrm{=}\mathrm{-}\mathrm{25}\mathrm{ } \\ \mathrm{ }\frac{\mathrm{x}}{\mathrm{2}}\mathrm{=}\frac{\mathrm{8}}{\mathrm{x}} \\ \mathrm{ }\frac{\mathrm{2}}{\mathrm{9}}{\mathrm{x}}^{\mathrm{2}}\mathrm{=}\mathrm{2} \\ \mathrm{ }\mathrm{5}\mathrm{+}\mathrm{2}{\mathrm{x}}^{\mathrm{2}}\mathrm{=}\mathrm{3} \\ } \end{gathered}$$

IV- Exercices

4-5/ Exercice 5

1. Simplifier les expressions suivantes :

$$\begin{gathered} \overline{) \\ \mathrm{ }\mathrm{A}\mathrm{=}\mathrm{(}\sqrt{\mathrm{75}}\mathrm{-}\sqrt{\mathrm{98}}\mathrm{)}\mathrm{(}\mathrm{5}\sqrt{\mathrm{3}}\mathrm{+}\mathrm{7}\sqrt{\mathrm{2}}\mathrm{)}\mathrm{=}\mathrm{ }\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{ } \\ \mathrm{ }\mathrm{B}\mathrm{=}{\mathrm{(}\mathrm{3}\mathrm{+}\sqrt{\mathrm{11}}\mathrm{)}}^{\mathrm{2}}\mathrm{-}{\mathrm{(}\mathrm{3}\mathrm{-}\sqrt{\mathrm{11}}\mathrm{)}}^{\mathrm{2}}\mathrm{=}\mathrm{ }\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{ } \\ \mathrm{ }\mathrm{C}\mathrm{=}\mathrm{(}\sqrt{\mathrm{3}}\mathrm{+}\sqrt{\mathrm{5}}\mathrm{-}\sqrt{\mathrm{7}}\mathrm{)}\mathrm{(}\sqrt{\mathrm{3}}\mathrm{+}\sqrt{\mathrm{5}}\mathrm{+}\sqrt{\mathrm{7}}\mathrm{)}\mathrm{=}\mathrm{ }\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{ } \\ \mathrm{ }\mathrm{D}\mathrm{=}\frac{\mathrm{2}\sqrt{\mathrm{27}}\mathrm{-}\mathrm{2}\sqrt{\mathrm{3}}\mathrm{+}\sqrt{\mathrm{12}}}{\sqrt{\mathrm{75}}\mathrm{+}\sqrt{\mathrm{48}}\mathrm{-}\mathrm{7}\sqrt{\mathrm{3}}}\mathrm{=}\mathrm{ } \\ } \end{gathered}$$

2. Écrire les quotients suivants sans radical au dénominateur :

$$\begin{gathered} \overline{) \\ \mathrm{ }\frac{\mathrm{1}}{\sqrt{\mathrm{7}}}\mathrm{=} \\ \mathrm{ }\frac{\sqrt{\mathrm{5}}}{\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{=} \\ \mathrm{ }\frac{\mathrm{-}\mathrm{10}}{\mathrm{3}\sqrt{\mathrm{5}}}\mathrm{=} \\ \mathrm{ }\frac{\mathrm{-}\mathrm{4}}{\mathrm{1}\mathrm{-}\sqrt{\mathrm{5}}}\mathrm{=} \\ \mathrm{ }\frac{\mathrm{2}\sqrt{\mathrm{3}}\mathrm{-}\mathrm{3}\sqrt{\mathrm{5}}}{\sqrt{\mathrm{5}}\mathrm{+}\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{=}\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ } \\ } \end{gathered}$$

IV- Exercices

4-6/ Exercice 6

On pose :

$$\begin{gathered} \overline{) \\ \mathrm{ }\mathrm{A}\mathrm{=}\mathrm{2}\mathrm{+}\mathrm{3}\sqrt{\mathrm{5}} \\ \mathrm{ }\mathrm{B}\mathrm{=}\mathrm{49}\mathrm{+}\mathrm{12}\sqrt{\mathrm{5}} \\ \mathrm{ }\mathrm{C}\mathrm{=}\mathrm{49}\mathrm{-}\mathrm{12}\sqrt{\mathrm{5}}\mathrm{ } \\ } \end{gathered}$$

1. Montrer que $\sqrt{B}=A$

2. Déduire $\sqrt{C}$

3. Calculer $\sqrt{B}\times \sqrt{C}$

4. Calculer $\sqrt{B}+\sqrt{C}$

5. Calculer $\sqrt{B}-\sqrt{C}$