Séance 7 - Noyaux, masse et énergie

Sommaire

I- Introduction

II- Équivalence entre masse et énergie

2-1/ L’énergie libérée lors d’une désintégration radioactive

2-2/ Le défaut de masse

2-3/ Relation d'Einstein

III- Unités de masse et d'énergie

3-1/ Unité de masse atomique

3-2/ Unité de l’énergie : ElectronVolt

3-3/ Énergie équivalente à l'unité de masse atomique

IV- Énergie de liaison d'un noyau

4-1/ Défaut de masse

4-2/ Énergie de liaison du noyau

4-3/ Énergie de liaison par nucléon

4-4/ Courbe d’Aston

V- La fission et la fusion nucléaires

5-1/ La fission nucléaire

5-2/ La fusion nucléaire

VI- Bilan énergétique d’une réaction nucléaire

6-1/ Cas général

6-2/ Diagramme énergétique d’une réaction nucléaire

6-3/ Bilan énergétique de la fission

6-4/ Bilan énergétique de la fusion

6-5/ Bilan énergétique des transformations nucléaires spontanées

VII- Exercices

7-1/ Exercice 1

7-2/ Exercice 2

7-3/ Exercice 3

7-4/ Exercice 4

I- Introduction

Une nébuleuse (du latin nebula, nuage) désigne, en astronomie, un objet céleste composé de gaz raréfié, ionisé et/ou de poussières interstellaires.

Avant les années 1920, le terme désignait tout objet du ciel d’aspect diffus.

La lumière de la nébuleuse Trifida nous parvient après un parcours de plusieurs centaines d’années de lumière.

• D’où provient l’énergie émise par une nébuleuse ?

II- Équivalence entre masse et énergie

2-1/ L’énergie libérée lors d’une désintégration radioactive

Considérons la désintégration spontanée du radium :

$\overline{)\mathrm{ }{}_{\mathrm{88}}{}^{\mathrm{226}}\mathrm{R}\mathrm{a}\mathrm{\to }{}_{\mathrm{86}}{}^{\mathrm{222}}\mathrm{R}\mathrm{n}\mathrm{+}{}_{\mathrm{2}}{}^{\mathrm{4}}\mathrm{H}\mathrm{e}\mathrm{+}\mathrm{\gamma }\mathrm{ }}$

Cette réaction nucléaire libère de l’énergie sous deux formes :

• De l’énergie cinétique : les particules produites sont émises avec une grande vitesse et possèdent donc de l’énergie cinétique.
• De l’énergie rayonnante : le rayonnement est une onde électromagnétique de très courte longueur d’onde et d’inertie élevée.

II- Équivalence entre masse et énergie

2-2/ Le défaut de masse

Effectuons le bilan de masse de la réaction nucléaire précédente :

• Avant la réaction : $m_{av}=m\left({}^{226}Ra\right)=3,752 4612\times {10}^{25}kg$
• Après la réaction : $m_{ap}=m\left({}^{222}Rn\right) +m\left({}_2{}^{4}He\right)=3,752 3747 x {10}^{25}Kg$

On constate que $m_{ap}<m_{av}$. Ce résultat est général :

Ce défaut de masse est faible en valeur relative :

$\overline{)\frac{m_{av}-m_{ap}}{m_{av}}=2.{10}^{-5}=0,002\%}$

II- Équivalence entre masse et énergie

2-3/ Relation d'Einstein

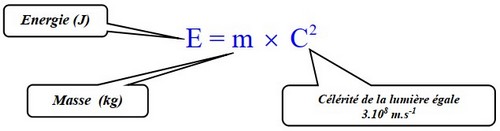
En 1905, Albert Einstein postulat l'équivalence entre la masse et l'énergie suivante :

« Tout corps de masse "m" au repos, possède une énergie égale au produit de sa masse par le carré de la vitesse de la lumière (c2) dans le vide».

III- Unités de masse et d'énergie

3-1/ Unité de masse atomique

En physique nucléaire, l'unité convenable de la masse s'appelle unité de masse atomique symbolisée par u, elle représente 1/12 de la masse d'un atome du carbone ${}_6{}^{12}C$

$\overline{)\mathrm{1}\mathrm{u}\mathrm{=}\frac{\mathrm{m}\left({}_6{}^{12}C\right)}{\mathrm{12}}\mathrm{=}\frac{\mathrm{M}\left({}_6{}^{12}C\right)}{\mathrm{12}\mathrm{\times }\mathrm{N}\mathrm{a}}\mathrm{=}\mathrm{1}\mathrm{,}\mathrm{66}\mathrm{.}{\mathrm{10}}^{\mathrm{-}\mathrm{27}}\mathrm{K}\mathrm{g}}$

3-2/ Unité de l’énergie : ElectronVolt

En physique nucléaire, on utilise fréquemment, comme unité d'énergie, l'électronVolt (eV) : $1eV=1,6.{10}^{-19}J$

On utilise aussi le méga-électronvolt : $1MeV={10}^{6}eV=1,6.{10}^{-13}J$

3-3/ Énergie équivalente à l'unité de masse atomique

D'après la relation d'Albert Einstein et pour la masse égale à 1 u on a :

$$\begin{gathered} \mathrm{E}\mathrm{=}\mathrm{m}\mathrm{\times }{\mathrm{C}}^{\mathrm{2}} \\ \mathrm{E}\mathrm{=}\mathrm{1}\mathrm{,}\mathrm{66054}\mathrm{.}{\mathrm{10}}^{\mathrm{-}\mathrm{27}}\mathrm{\times }{\left(299792458\right)}^{\mathrm{2}} \\ \mathrm{E}\mathrm{=}\mathrm{1492}\mathrm{,}\mathrm{42}\mathrm{.}{\mathrm{10}}^{\mathrm{-}\mathrm{13}}\mathrm{J} \\ \mathrm{E}\mathrm{=}\frac{\mathrm{1492}\mathrm{,}\mathrm{42}\mathrm{.}{\mathrm{10}}^{\mathrm{-}\mathrm{13}}}{\mathrm{1}\mathrm{,}\mathrm{602177}\mathrm{.}{\mathrm{10}}^{\mathrm{-}\mathrm{13}}}\mathrm{M}\mathrm{e}\mathrm{V} \\ \mathrm{E}\mathrm{=}\mathrm{931}\mathrm{,}\mathrm{5}\mathrm{ }\mathrm{M}\mathrm{e}\mathrm{V} \\ \mathrm{\Rightarrow }\overline{)\mathrm{1}\mathrm{u}\mathrm{=}\mathrm{931}\mathrm{,}\mathrm{5}\mathrm{ }\mathrm{M}\mathrm{e}\mathrm{V}\mathrm{/}{\mathrm{C}}^{\mathrm{2}}} \end{gathered}$$

IV- Énergie de liaison d'un noyau

4-1/ Défaut de masse

Des mesures précises effectuées à l’aide d’un spectrographe de masse montrent que la masse du noyau d’un atome est toujours inférieure à la somme des masse de ses nucléons pris individuellement.

Le défaut de masse d'un noyau de symbole  est la différence entre la masse des nucléons isolés et au repos est la masse du noyau au repos, on le symbolise par :

$\overline{)\mathrm{\Delta }\mathrm{m}\mathrm{=}\mathrm{Z}\mathrm{\times }{\mathrm{m}}_{\mathrm{p}}\mathrm{+}(A-Z)\mathrm{\times }{\mathrm{m}}_{\mathrm{n}}\mathrm{-}\mathrm{m}\left({}_Z{}^{A}X\right)}$

IV- Énergie de liaison d'un noyau

4-2/ Énergie de liaison du noyau

L’énergie de liaison Eℓ d’un noyau atomique est l'énergie qu'il faut fournir au noyau au repos pour le dissocier en ses nucléons constitutifs pris au repos :

$\overline{)\mathrm{ }{\mathrm{E}}_{\mathrm{L}}\mathrm{=}\mathrm{\Delta m}\mathrm{\times }{\mathrm{C}}^{\mathrm{2}}\mathrm{=}\mathrm{[}\mathrm{Z}\mathrm{\times }{\mathrm{m}}_{\mathrm{p}}\mathrm{+}\mathrm{(}\mathrm{A}\mathrm{-}\mathrm{Z}\mathrm{)}\mathrm{\times }{\mathrm{m}}_{\mathrm{n}}\mathrm{-}\mathrm{m}\mathrm{\left(}{}_{\mathrm{Z}}{}^{\mathrm{A}}\mathrm{X}\mathrm{\right)}\mathrm{]}\mathrm{\times }{\mathrm{C}}^{\mathrm{2}}\mathrm{>}\mathrm{0}\mathrm{ }}$

4-3/ Énergie de liaison par nucléon

Parfois on utilise l'énergie de liaison par nucléon qui est donnée par la relation suivante :

$\mathrm{\xi }\mathrm{=}\frac{{\mathrm{E}}_{\mathrm{L}}}{\mathrm{A}}$

L'énergie de liaison est exprimée en MeV/nucléon

Un noyau est d'autant plus stable que son énergie de liaison par nucléon est grande.

IV- Énergie de liaison d'un noyau

4-4/ Courbe d’Aston

La courbe d'Aston est une courbe représentant l’opposée de l'énergie de liaison par nucléon des noyaux atomiques, en fonction de leur nombre de nucléons :

Cette courbe permet de comparer la stabilité des différents noyaux atomiques.

V- La fission et la fusion nucléaires

5-1/ La fission nucléaire

La fission est une transformation nucléaire au cours de laquelle un noyau lourd bombardé par un neutron se divise en deux noyaux plus petits :

On utilise le neutron dans le bombardement car c'est une particule neutre qui arrive facilement au noyau sans entrer en répulsion avec lui.

V- La fission et la fusion nucléaires

5-2/ La fusion nucléaire

La fusion est une réaction nucléaire au cours de laquelle deux noyaux légers s’unissent pour former un noyau lourd :

La fusion est une réaction nucléaire provoquée qui libère de l’énergie.

VI- Bilan énergétique d’une réaction nucléaire

6-1/ Cas général

On considère une transformation nucléaire quelconque :

$\overline{)\mathrm{ }{}_{{\mathrm{Z}}_{\mathrm{1}}}{}^{{\mathrm{A}}_{\mathrm{1}}}\mathrm{X}_{\mathrm{1}}\mathrm{+}{}_{{\mathrm{Z}}_{\mathrm{2}}}{}^{{\mathrm{A}}_{\mathrm{2}}}\mathrm{X}_{\mathrm{2}}\mathrm{\to }{}_{{\mathrm{Z}}_{\mathrm{3}}}{}^{{\mathrm{A}}_{\mathrm{3}}}\mathrm{X}_{\mathrm{3}}\mathrm{+}{}_{{\mathrm{Z}}_{\mathrm{4}}}{}^{{\mathrm{A}}_{\mathrm{4}}}\mathrm{X}_{\mathrm{4}}\mathrm{ }}$

${\mathrm{X}}_{\mathrm{i}}$ représente un noyau ou une particule.

Le bilan énergétique correspond à cette réaction est :

$\overline{)\mathrm{ }\mathrm{\Delta }\mathrm{E}\mathrm{ }\mathrm{=}[E_L\left(X_1\right)+E_L\left(X_2\right)]\mathrm{-}[E_L\left(X_3\right)+E_L\left(X_4\right)]\mathrm{ }}$

où ${\mathrm{E}}_{\mathrm{L}}\left(X_i\right)$ l’énergie de liaison d’un noyau ou particule ${\mathrm{X}}_{\mathrm{i}}$ et $\mathrm{\Delta E}$ l’énergie de la réaction

$E_{libérée}=\left|\mathrm{\Delta E}\right|$

et d’après l’expression de l’énergie de liaison d’un noyau on obtient :

$$\begin{gathered} \mathrm{\Delta E}\mathrm{ }\mathrm{=}\mathrm{\{}\mathrm{[}\mathrm{m}\left(X_3\right)\mathrm{+}\mathrm{m}\left(X_4\right)\mathrm{]}\mathrm{-}\mathrm{[}\mathrm{m}\left(X_1\right)\mathrm{+}\mathrm{m}\left(X_2\right)\mathrm{]}\mathrm{\}}\mathrm{.}{\mathrm{c}}^{\mathrm{2}} \\ \overline{)\mathrm{\Delta E}\mathrm{ }\mathrm{=}\mathrm{\sum }_{\mathrm{i}\mathrm{=}\mathrm{1}}^{\mathrm{n}}[m_i\left(produits\right)-m_i\left(\mathrm{réactifs}\right)]\mathrm{.}{\mathrm{c}}^{\mathrm{2}}} \end{gathered}$$

VI- Bilan énergétique d’une réaction nucléaire

6-2/ Diagramme énergétique d’une réaction nucléaire

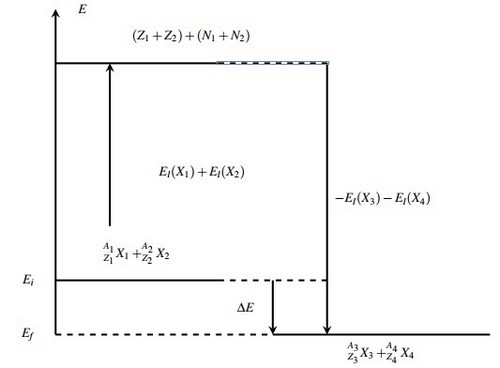
${\mathrm{E}}_{\mathrm{i}}$ : L’énergie initiale su système.

${\mathrm{E}}_{\mathrm{f}}$ : L’énergie finale du système

${\mathrm{E}}_{\mathrm{L}}\left(X_1\right)\mathrm{+}{\mathrm{E}}_{\mathrm{L}}\left(X_2\right)$ : L’énergie reçue par le système pour séparer les deux noyaux ${\mathrm{X}}_{\mathrm{1}}$ et ${\mathrm{X}}_2$.

$\mathrm{-}{\mathrm{E}}_{\mathrm{L}}\mathrm{\left(}{\mathrm{X}}_{\mathrm{3}}\mathrm{\right)}\mathrm{-}{\mathrm{E}}_{\mathrm{L}}\mathrm{\left(}{\mathrm{X}}_{\mathrm{4}}\mathrm{\right)}$ : L’énergie libérées par le système lors de la formation des noyaux ${\mathrm{X}}_3$ et ${\mathrm{X}}_4$

${\mathrm{E}}_{\mathrm{l}\mathrm{i}\mathrm{b}}\mathrm{=}\left|\Delta E\right|$ : L’énergie de la réaction est l’énergie libérée par le système pour qu’ils soient plus stable et elle est considérée positive

VI- Bilan énergétique d’une réaction nucléaire

6-3/ Bilan énergétique de la fission

On considère la fission nucléaire de l’uranium 235 suivante :

$\overline{)\mathrm{ }{}_{\mathrm{92}}{}^{\mathrm{235}}\mathrm{U}\mathrm{+}{}_{\mathrm{0}}{}^{\mathrm{1}}\mathrm{n}\mathrm{\to }{}_{\mathrm{38}}{}^{\mathrm{94}}\mathrm{S}\mathrm{r}\mathrm{+}{}_{\mathrm{54}}{}^{\mathrm{139}}\mathrm{X}\mathrm{e}\mathrm{+}\mathrm{3}{}_{\mathrm{0}}{}^{\mathrm{1}}\mathrm{n}\mathrm{+}\mathrm{\gamma }\mathrm{ }}$

$$\begin{gathered} m\left({}_{92}{}^{235}U\right)=234,99332u \\ m\left({}_{38}{}^{94}Sr\right)=93,8944u \\ m\left({}_{54}{}^{139}Xe\right)=138,89194u \\ m\left({}_0{}^{1}n\right)=1,00866u \end{gathered}$$

L’énergie produite au cours de cette réaction nucléaire est :

$$\begin{gathered} \mathrm{\Delta }\mathrm{E}\mathrm{=}[m\left(Sr\right)+m\left(Xe\right)+2m\left(n\right)-m\left(U\right)]\mathrm{.}{\mathrm{c}}^{\mathrm{2}} \\ \overline{)\mathrm{\Delta }\mathrm{E}\mathrm{=}\mathrm{-}\mathrm{0}\mathrm{,}\mathrm{1896}\mathrm{u}\mathrm{.}{\mathrm{c}}^{\mathrm{2}}} \end{gathered}$$

VI- Bilan énergétique d’une réaction nucléaire

6-4/ Bilan énergétique de la fusion

On considère la réaction de fusion nucléaire suivante :

$\overline{)\mathrm{ }{}_{\mathrm{1}}{}^{\mathrm{2}}\mathrm{H}\mathrm{+}{}_{\mathrm{1}}{}^{\mathrm{3}}\mathrm{H}\mathrm{\to }{}_{\mathrm{2}}{}^{\mathrm{4}}\mathrm{He}\mathrm{+}{}_{\mathrm{0}}{}^{\mathrm{1}}\mathrm{n}\mathrm{ }}$

On donne :

$$\begin{gathered} m\left({}_1{}^{2}H\right)=2,01355u \\ m\left({}_1{}^{3}H\right)=3,0155u \\ m\left({}_2{}^{4}He\right)=4,0015u \\ m\left({}_0{}^{1}n\right)=1,00866u \end{gathered}$$

L’énergie produite au cours de cette réaction nucléaire est :

$$\begin{gathered} \mathrm{\Delta }\mathrm{E}\mathrm{=}\mathrm{[}\mathrm{m}\left(\mathrm{He}\right)\mathrm{+}\mathrm{m}\left(n\right)\mathrm{-}\mathrm{m}\left({}^{3}H\right)\mathrm{-}\mathrm{m}\left({}^{2}H\right)\mathrm{]}\mathrm{.}{\mathrm{c}}^{\mathrm{2}} \\ \overline{)\mathrm{\Delta }\mathrm{E}\mathrm{=}\mathrm{-}\mathrm{17}\mathrm{,}\mathrm{585}\mathrm{MeV}} \end{gathered}$$

VI- Bilan énergétique d’une réaction nucléaire

6-5/ Bilan énergétique des transformations nucléaires spontanées

Bilan énergétique de la transformation $\mathrm{\alpha }$

$\overline{){}_{\mathrm{Z}}{}^{\mathrm{A}}\mathrm{X}\mathrm{\to }{}_{\mathrm{Z}\mathrm{-}\mathrm{2}}{}^{\mathrm{A}\mathrm{-}\mathrm{4}}\mathrm{Y}\mathrm{+}{}_{\mathrm{2}}{}^{\mathrm{4}}\mathrm{H}\mathrm{e}}$

Bilan énergétique de la transformation ${\mathrm{\beta }}^{\mathrm{-}}$

$\overline{){}_{\mathrm{Z}}{}^{\mathrm{A}}\mathrm{X}\mathrm{\to }{}_{\mathrm{Z}\mathrm{+}\mathrm{1}}{}^{\mathrm{A}}\mathrm{Y}\mathrm{+}{}_{\mathrm{-}\mathrm{1}}{}^{\mathrm{0}}\mathrm{e}}$

Bilan énergétique de la transformation ${\mathrm{\beta }}^{\mathrm{+}}$

Elle ressemble à celle de la transformation ${\mathrm{\beta }}^{\mathrm{-}}$

VII- Exercices

7-1/ Exercice 1

On considère la réaction suivante, qui est l’une des nombreuses réactions de fission de l’uranium 235 se produisant dans le cœur des centrales nucléaires :

$\overline{)\mathrm{ }{}_{\mathrm{0}}{}^{\mathrm{1}}\mathrm{n}\mathrm{+}{}_{\mathrm{92}}{}^{\mathrm{235}}\mathrm{U}\mathrm{\to }{}_{\mathrm{55}}{}^{\mathrm{140}}\mathrm{C}\mathrm{s}\mathrm{+}{}_{\mathrm{x}}{}^{\mathrm{93}}\mathrm{R}\mathrm{b}\mathrm{+}\mathrm{y}\mathrm{.}{}_{\mathrm{0}}{}^{\mathrm{1}}\mathrm{n}\mathrm{ }}$

1. Déterminer x et y de manière à équilibrer cette réaction .
2. Quelle est l’énergie produite par cette réaction ?
3. Quelle est l’énergie produite par la fission d’un gramme d’uranium 235 ?
4. Pendant combien de temps la fission d’un gramme d’uranium 235 permet - elle de délivrer une puissance d’un mégawatt (On suppose que le rendement est 100%) ?

Données:

$N_A=6,02\times {10}^{23}mo{l}^{-1}$

VII- Exercices

7-2/ Exercice 2

Les « combustibles » utilisés dans le réacteur de fusion ne nécessitent pas de transport de matière radioactive.

En effet, le deutérium n’est pas radioactif. Le tritium est fabriqué sur site, à partir d’un élément Y non radioactif suivant la réaction :

$Y+{}_0{}^{1}n\to {}_2{}^{4}He+{}_1{}^{3}H$

1) Le tritium

1. Donner la composition et le symbole du noyau Y en précisant les règles de conservation.

On donne un extrait de la classification périodique : $H (Z=1) ; He (Z=2) ; Li (Z=3) ; Be (Z=4) ; B (Z=5)$.

2) Le noyau de deutérium

2. 1- Donner la composition du noyau de deutérium ${}_1{}^{2}H$.

2. 2- Le deutérium et le tritium sont des isotopes. Justifier cette affirmation.

2. 3- Donner l’expression littérale puis la valeur du défaut de masse $\Delta m\left({}_1{}^{2}H\right)$ du noyau de deutérium.

2. 4- En déduire l’énergie $E\left({}_1{}^{2}H\right)$ correspondant à ce défaut de masse en J puis en MeV et donner sa signification physique.

3) Étude de la réaction de fusion ${}_1{}^{2}H+{}_1{}^{3}H\to {}_2{}^{4}He+{}_0{}^{1}n$

3. Donner l’expression littérale de l’énergie libérée par cette réaction en fonction des données de l’énoncé et calculer cette énergie en MeV.

4) Ressources en deutérium

On trouve le deutérium en abondance dans l’eau de mer. La ressource dans les océans est estimée à $4,6\times {10}^{13}$ tonnes.

La réaction (1) libère une énergie de $17,6 MeV$.

On assimile la masse d’un atome de deutérium à la masse de son noyau.

4. 1-1- Déterminer le nombre N de noyaux présents dans la masse $m=1,0Kg$ de deutérium.

4. 1-2- En déduire l’énergie E libérée par une masse $m=1,0Kg$ de deutérium.

La consommation annuelle énergétique mondiale actuelle est d’environ $4\times {10}^{20}J$.

On fait l’hypothèse simplificatrice selon laquelle le rendement d’une centrale à fusion est équivalent à celui d’une centrale nucléaire.

Ceci revient à considérer que seule 33% de l’énergie libérée par la réaction de fusion est réellement convertie en électricité.

4. 2- Estimer en années, la durée $\Delta t$ nécessaire pour épuiser la réserve de deutérium disponible dans les océans répondant à la consommation annuelle actuelle.

Données :

• Masse du neutron : $m\left(n\right)=1,674927.{10}^{-27}Kg$
• Masse du proton : $m\left(p\right)=1,672622.{10}^{-27}Kg$
• $$\begin{gathered} m\left({}_1{}^{2}H\right)=3,344497.{10}^{-27 }Kg \\ m\left({}_1{}^{3}H\right)=5,008271.{10}^{-27 }Kg \\ m\left({}_2{}^{4}H\right)=6,646483.{10}^{-27} Kg \\ 1u=931,5 MeV/c^2 \\ 1eV=1,60.{10}^{-19} J \\ C=3.{10}^8 m/s \end{gathered}$$

VII- Exercices

7-3/ Exercice 3

L’énergie dégagée au cours de la combustion complète d’une mole de butane est $Q=2878\times {10}^3 J$, ça veut dire que la combustion complète de $56 g$ de butane dégage une énergie de $Q=2878\times {10}^3 J$.

Fission nucléaire

Une centrale nucléaire est une usine de production d'électricité.

Actuellement ces centrales utilisent la chaleur libérée par des réactions de fission de l'uranium 235 qui constitue le "combustible nucléaire". Cette chaleur transforme de l'eau en vapeur. La pression de la vapeur permet de faire tourner à grande vitesse une turbine qui entraîne un alternateur produisant l'électricité.

Certains produits de fission sont des noyaux radioactifs à forte activité et dont la demi-vie peut être très longue.

1. Définir le terme demi-vie.

Le bombardement d'un noyau d'uranium 235 par un neutron peut produire un noyau de strontium et un noyau de xénon selon l'équation suivante :

$\overline{) {}_{92}{}^{235}U+ {}_0{}^{1}n\to {}_Z{}^{94}Sr+ {}_{54}{}^{A}Xe+3 {}_0{}^{1}n }$

2. Déterminer les valeurs des nombres A et Z.

3. Calculer en MeV puis en joule l'énergie libérée par la fission d’un noyau d’uranium 235.

4. Déduire L’énergie libérée en joule par la fission d’une mole d’uranium 235.

5. Quelle est la masse de butane qu’on doit utiliser au cours d’une combustion complète pour produire la même quantité d’énergie libérée lors de la fission de $235 g$ d’uranium ${}^{235}U$ ?

Fusion nucléaire

La fusion est la source d'énergie du soleil et des autres étoiles.

Pour obtenir une réaction de fusion, il faut rapprocher suffisamment deux noyaux qui se repoussent, puisqu'ils sont tous deux chargés positivement. Une certaine énergie est donc indispensable pour franchir cette barrière et arriver dans la zone, très proche du noyau, où se manifestent les forces nucléaires capables de l'emporter sur la répulsion électrostatique.

La réaction de fusion la plus accessible est la réaction impliquant le deutérium et le tritium : C'est sur cette réaction que se concentrent les recherches concernant la fusion contrôlée.

La demi-vie du tritium consommé au cours de cette réaction n'est que de quelques années. De plus il y a très peu de déchets radioactifs générés par la fusion et l'essentiel est retenu dans les structures de l'installation.

Le deutérium de symbole ${}_1{}^{2}H$ et le tritium de symbole ${}_1{}^{3}H$ sont deux isotopes de l'hydrogène.

1. 1- Définir le terme de noyaux isotopes.

1. 2- Donner la composition de ces deux noyaux.

2. Qu'appelle-t-on réaction de fusion ?

3. Écrire l'équation de la réaction nucléaire entre un noyau de Deutérium et un noyau de Tritium sachant que cette réaction libère un neutron et un noyau noté ${}_Z{}^{A}X$. Préciser la nature du noyau ${}_Z{}^{A}X$.

4. Montrer que l'énergie libérée au cours de cette réaction de fusion est de $17,6 MeV$.

5. Quelle est l'énergie libérée par la fusion d’une mole de tritium ?

6. Quelle est la masse de butane qu’on doit utiliser au cours d’une combustion complète pour produire la même quantité d’énergie libérée lors de la fusion d’une mole de tritium ?

Donneés :

• Unité de masse atomique : $\mu =1,66\times {10}^{-27} kg$
• Énergie de masse de l'unité de masse atomique : $1\mu =931,5 MeV.C^{-2}$
• Électronvolt : $1eV = 1,60\times {10}^{-19} J$
• Vitesse de la lumière dans le vide : $c=3,00\times 108 m.s^{-1}$
• Nombre d’Avogadro : $N_A=6,02.{10}^{23}$

VII- Exercices

7-4/ Exercice 4

Dans une centrale nucléaire, les noyaux d'uranium ${}_{92}{}^{235}U$ subissent la fission sous le choc d'un neutron lent.

Un des nombreux processus possibles conduit à la formation d'un noyau de lanthane ${}_{57}{}^{144}La$, d'un noyau de brome ${}_{35}{}^{88}Br$ et de plusieurs neutrons.

1. Définissez l'énergie de liaison d'un noyau.

2. Donnez l'expression littérale qui permettra son calcul.

3. Calculez, en MeV, l'énergie de liaison d’un noyau ${}_{92}{}^{235}U$.

4. Calculez l’énergie de liaison par nucléon de ce noyau.

5. Écrivez l’équation de la réaction de fission étudiée.

6. Exprimez l'énergie libérée par la fission d'un noyau ${}_{92}{}^{235}U$ en fonction des énergies de liaison par nucléon du noyau père et des noyaux fils et calculez la valeur de cette énergie en MeV.

Dans le cœur de la centrale, de nombreuses autres réactions de fission du noyau ${}_{92}{}^{235}U$ se produisent, la perte de masse est, en moyenne, de 0,200 u par noyau.

7. 1- Calculez, en MeV, l'énergie moyenne libérée par la fission d’un noyau. Ce résultat est-il en concordance avec celui de la question 6 ?

7. 2- Calculez, en joule, l'énergie moyenne libérée par une mole de noyaux ${}_{92}{}^{235}U$.

Dans une centrale nucléaire, l’énergie nucléaire est transformée en énergie électrique. Une centrale fournit une puissance électrique moyenne $P_e=1000 MW$ avec un rendement r = 25%.

8. 1- Quelle est sa puissance nucléaire $P_n$ consommée ?

8. 2- Quelle est, en joule, l'énergie nucléaire consommée chaque année ? 8-3/ Quelle est, en tonne, la masse d’uranium 235 consommée annuellement ?

Données :

• Constante d'Avogadro : $N_A = 6,02.{10}^{23} mo{l}^{-1}$
• $1\mu =1,66055. {10}^{-27}kg$ et $1MeV=1,602.{10}^{-13}J$
• Masse d’un proton : $m\left(p\right)=1,0073\mu$
• Masse d’un neutron : $m\left(n\right)=1,0087\mu$
• Célérité de la lumière dans le vide : $c=2,998\times 108m.s^{-1}$
• Masse du noyau d’uranium 235 : $m\left({}_{92}{}^{235}U\right)=235,0134\mu$
• Énergie de liaison par nucléon : $E_l/A\left({}_{57}{}^{144}La\right)=8,28MeV/nucléon$
• Énergie de liaison par nucléon : $E_l/A\left({}_{35}{}^{88}Br\right)=8,56MeV/nucléon$