Séance 5 - Suivi temporel d’une transformation chimique – Vitesse de réaction

Sommaire

I- Techniques du suivi temporel d’une transformation

II- Suivi temporel d’une transformation

2-1/ Méthode de dosage

2-2/ Méthode de mesure de la pression

2-3/ Méthode de mesure de la conductance

III- Vitesse de réaction – Temps de demi-réaction

3-1/ Vitesse de réaction

3-2/ Temps de demi réaction

3-3/ Vitesse de réaction et facteurs cinétiques

IV- Exercices

4-1/ Exercice 1

4-2/ Exercice 2

4-3/ Exercice 3

4-4/ Exercice 4

I- Techniques du suivi temporel d’une transformation

Pour effectuer le suivi temporel d’une transformation se déroulant à volume constant, on mesure à différents instants successifs la concentration d’un réactif ou d’un produit dans le milieu réactionnel, en pratiquant une des méthodes chimiques et physiques suivants :

• Le dosage.
• La conductimétrie.
• La mesure de la pression.
• La pH-métrie.

II- Suivi temporel d’une transformation

2-1/ Méthode de dosage

Définition

Le dosage est l'action qui consiste à déterminer la quantité de matière, la fraction, ou la concentration d'une substance précise présente dans une autre ou dans un mélange.

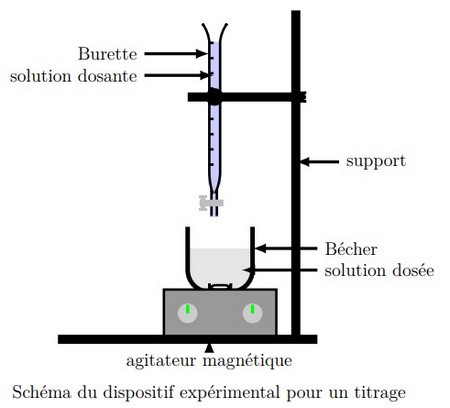
Expérience

On réalise le mélange suivant:

On verse, dans un bécher, un volume ${\mathrm{V}}_{\mathrm{1}}\mathrm{=}\mathrm{100}\mathrm{m}\mathrm{l}$ d’une solution d’iodure de potassium $(K^{+}+I^{-})$ de concentration ${\mathrm{C}}_{\mathrm{1}}\mathrm{=}\mathrm{0}\mathrm{,}\mathrm{4}\mathrm{ }\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{/}\mathrm{L}$

Puis on ajoute un volume ${\mathrm{V}}_{\mathrm{2}}\mathrm{=}\mathrm{100}\mathrm{m}\mathrm{l}$ d’une solution de peroxodisufate de potassium $(2K^{+}+S_2{O_8}^{2-})$ de concentration ${\mathrm{C}}_2\mathrm{=}\mathrm{0}\mathrm{,}\mathrm{036}\mathrm{ }\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{/}\mathrm{L}$ acidifié par $\mathrm{1}\mathrm{m}\mathrm{l}$ d’acide sulfurique concentré.

$$\begin{gathered} \overline{)S_2{O_8}^{2-} + 2e^{-} \to 2{{\mathrm{SO}}_4}^{2-} \\ 2I^{-} \to I_2+ 2e^{-}} \end{gathered}$$

Dosage

Pour savoir la quantité du diiode qui s'est formée à un instant donné on réalise le dosage de la manière suivante:

On recueille après chaque trois minutes $\mathrm{10}\mathrm{m}\mathrm{l}$ du mélange réactionnel et on la trempe dans l'eau froide pour arrêter la réaction.

Puis on dose le diode ${\mathrm{I}}_{\mathrm{2}}$ formé par une solution de thiosulfate de sodium $(2N{a}^{+}+S_2{O_3}^{2-})$ de concentration ${\mathrm{C}}_r\mathrm{=}\mathrm{0}\mathrm{,}\mathrm{02}\mathrm{ }\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{/}\mathrm{L}$

$\overline{)2S_2{O_3}^{2-} + I_2 \to {S_4{O}_6}^{2-}+2I^{-}}$

On refait les opérations précédentes à différents instants, comme l’indique le tableau suivant :

II- Suivi temporel d’une transformation

2-1/ Méthode de dosage

Exploitation

Tableau d’avancement:

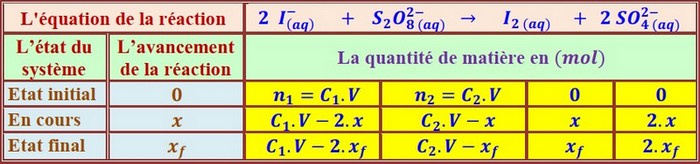
D'après le tableau d'avancement, la quantité du diiode formée à un instant t est égale à x :  $n{\left(I_2\right)}_t=x$

Donc le dosage nous permet de suivre l'évolution de la formation du diiode en fonction du temps et de déterminer l'avancement.

Le tracé montre que la quantité du diiode formée augmente en fonction du temps.

On peut déterminer les quantités de matières des autres constituants du mélange réactionnel en fonction du temps.

par exemple: $\overline{)\mathrm{n}\left(S_2{O_8}^{2-}\right)\mathrm{=}{\mathrm{C}}_{\mathrm{2}}\mathrm{.}{\mathrm{V}}_{\mathrm{2}}\mathrm{-}\mathrm{x}\mathrm{=}\mathrm{3}\mathrm{,}\mathrm{6}\mathrm{-}\mathrm{x}}$

Tableau des mesures:

Variation de $\mathrm{n}\mathrm{\left(}{\mathrm{S}}_{\mathrm{2}}{{\mathrm{O}}_{\mathrm{8}}}^{\mathrm{2}\mathrm{-}}\mathrm{\right)}$ en fonction du temps:

II- Suivi temporel d’une transformation

2-2/ Méthode de mesure de la pression

Expérience

On introduit un ruban de magnésium de masse $\mathrm{m}\mathrm{=}\mathrm{0}\mathrm{,}\mathrm{02}\mathrm{ }\mathrm{g}$ dans un ballon contenant un volume $\mathrm{V}\mathrm{=}\mathrm{50}\mathrm{ }\mathrm{c}{\mathrm{m}}^{\mathrm{3}}$ d'une solution d'acide chlorhydrique $({H^{+}}_{\left(aq\right)}+C{l^{-}}_{\left(aq\right)})$ de concentration $\mathrm{C}\mathrm{=}\mathrm{0}\mathrm{,}\mathrm{5}\mathrm{ }\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{/}\mathrm{l}$ puis on mesure la pression du gaz résultant par un manomètre.

On constate que le magnésium réagit avec l'acide chlorhydrique avec dégagement d'hydrogène et cette réaction dure quelques minutes jusqu'à la disparition totale du ruban de magnésium.

$\overline{)\mathrm{M}{\mathrm{g}}_{\left(s\right)}\mathrm{+}\mathrm{2}{{\mathrm{H}}^{\mathrm{+}}}_{\left(\mathrm{aq}\right)}\mathrm{\to }\mathrm{ }\mathrm{M}{{\mathrm{g}}^{\mathrm{2}\mathrm{+}}}_{\left(\mathrm{aq}\right)}\mathrm{+}{\mathrm{H}}_{{\mathrm{2}}_{\left(g\right)}}}$

II- Suivi temporel d’une transformation

2-2/ Méthode de mesure de la pression

Exploitation

Tableau d’avancement:

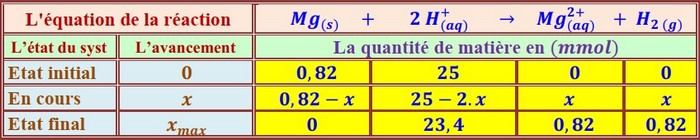
Tableau des mesures:

Représentation de la variation de $\mathrm{n}\left(H_2\right)$ en fonction du temps:

II- Suivi temporel d’une transformation

2-3/ Méthode de mesure de la conductance

Expérience

On introduit dans un bécher un peu d'eau et d'éthanol et on ajoute au mélange $\mathrm{1}\mathrm{ }\mathrm{c}{\mathrm{m}}^{\mathrm{3}}$ de 2-chloro 2-méthyle propane de formule semi-développée : ${\left(C{H}_3\right)}_{\mathrm{3}}\mathrm{—}\mathrm{C}\mathrm{—}\mathrm{C}\mathrm{l}$ qu’on notera simplement RCL.

L'éthanol est un solvant dans lequel RCL se dissout très facilement et sans réagir avec l'éthanol.

RCL réagit avec l'eau selon l'équation suivante:

$\overline{)\mathrm{R}\mathrm{C}\mathrm{L}\mathrm{ }\mathrm{+}\mathrm{ }{\mathrm{H}}_{\mathrm{2}}{\mathrm{O}}_{\left(l\right)}\mathrm{ }\mathrm{\to }\mathrm{ }\mathrm{R}\mathrm{O}\mathrm{H}\mathrm{+}{{\mathrm{H}}^{\mathrm{+}}}_{\left(\mathrm{aq}\right)}\mathrm{+}\mathrm{C}{{\mathrm{l}}^{\mathrm{-}}}_{\left(\mathrm{aq}\right)}}$

La formation des ions ${\mathrm{H}}^{\mathrm{+}}$ et ${\mathrm{C}\mathrm{l}}^{\mathrm{-}}$ entraine l'augmentation de la conductance de la solution.

On mesure la conductance du mélange réactionnel chaque 200s, ce qui permet de déterminer la variation de sa conductivité en fonction du temps.

II- Suivi temporel d’une transformation

2-3/ Méthode de mesure de la conductance

Exploitation

Tableau d’avancement:

$\overline{)\mathrm{\sigma }\mathrm{=}{\mathrm{\lambda }}_{\left(H^{+}\right)}\mathrm{\left[}{\mathrm{H}}^{\mathrm{+}}\mathrm{\right]}\mathrm{+}{\mathrm{\lambda }}_{\left({\mathrm{Cl}}^{-}\right)}\mathrm{\left[}{\mathrm{Cl}}^{\mathrm{-}}\mathrm{\right]}}$

$\overline{)\mathrm{x}\left(t\right)\mathrm{=}{\mathrm{x}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\mathrm{.}\frac{\mathrm{\sigma }\left(t\right)}{{\mathrm{\sigma }}_{\mathrm{m}\mathrm{a}\mathrm{x}}}}$

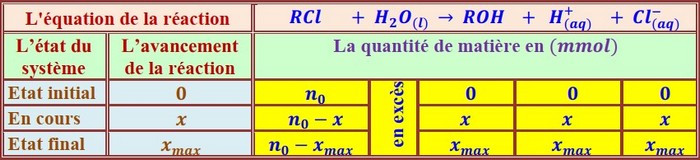
Tableau des mesures:

Représentation de la variation de $\mathrm{x}$ en fonction du temps:

III- Vitesse de réaction – Temps de demi-réaction

3-1/ Vitesse de réaction

Définition

La vitesse volumique d’une réaction correspond à la quantité de matière formée ou disparue par unité de temps et de volume.

Elle est liée à la variation de l’avancement x de la réaction en fonction du temps par la relation suivante:

$\overline{)\mathrm{\nu }\mathrm{=}\frac{\mathrm{1}}{\mathrm{V}}\frac{\mathrm{d}\mathrm{x}}{\mathrm{d}\mathrm{t}}}$

Elle peut être exprimer en : $\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{/}{\mathrm{m}}^{\mathrm{3}}\mathrm{.}\mathrm{s}$ dans le SI, ou $\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{/}\mathrm{L}\mathrm{.}\mathrm{m}\mathrm{i}\mathrm{n}$ ou $\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{/}\mathrm{L}\mathrm{.}\mathrm{s}$

En général, la vitesse de la réaction diminue lors de l'évolution d'une transformation chimique.

III- Vitesse de réaction – Temps de demi-réaction

3-1/ Vitesse de réaction

Détermination graphique de la vitesse de la réaction

On détermine la vitesse de la réaction à un instant t donné, en traçant la droite tangente à la courbe x=f(t) à cet instant puis on détermine le coefficient directeur de cette droite et on le divise par le volume V de la solution.

Évolution de la vitesse de réaction au cours du temps

On remarque la diminution de l'angle $\mathrm{\alpha }$ et par conséquent les valeurs de coefficient directeur de la tangente $\mathrm{t}\mathrm{a}\mathrm{n}\left(\alpha \right)$ diminuent au fur et à mesure que la transformation évolue avec le temps.

Et puisque la transformation se déroule dans un volume constant, alors la vitesse de réaction diminue avec le temps.

III- Vitesse de réaction – Temps de demi-réaction

3-2/ Temps de demi réaction

Définition

On appelle temps de demi-réaction ${\mathrm{t}}_{\mathrm{1}\mathrm{/}\mathrm{2}}$ le temps nécessaire pour que l'avancement de la réaction soit égal à la moitié de sa valeur finale

$\overline{)\mathrm{x}\left(t_{1/2}\right)\mathrm{=}\frac{{\mathrm{x}}_{\mathrm{f}}}{\mathrm{2}}}$

Si la réaction est totale, alors ${\mathrm{x}}_{\mathrm{f}}\mathrm{=}{\mathrm{x}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ , dans ce cas on a : $\mathrm{x}\mathrm{\left(}{\mathrm{t}}_{\mathrm{1}\mathrm{/}\mathrm{2}}\mathrm{\right)}\mathrm{=}\frac{{\mathrm{x}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{\mathrm{2}}$

Détermination graphique du temps de demi-réaction

III- Vitesse de réaction – Temps de demi-réaction

3-3/ Vitesse de réaction et facteurs cinétiques

Plus la température est élevée, plus les risques de collisions sont élevés et plus la réaction est rapide.

Plus les concentrations initiales de réactifs sont élevées, plus la probabilité de collisions est grande et donc plus la réaction est rapide.

IV- Exercices

4-1/ Exercice 1

Deux groupes d’élèves veulent étudier l’évolution dans le temps de la réaction d’oxydation des ions iodure ${\mathrm{I}}^{\mathrm{-}}$ par les ions peroxodisulfate ${\mathrm{S}}_{\mathrm{2}}{{\mathrm{O}}_{\mathrm{8}}}^{\mathrm{2}\mathrm{-}}$ dans deux conditions expérimentales différentes.

L’équation de cette réaction est :

$\overline{)\mathrm{2}{\mathrm{I}}^{\mathrm{-}}\mathrm{+}{\mathrm{S}}_{\mathrm{2}}{{\mathrm{O}}_{\mathrm{8}}}^{\mathrm{2}\mathrm{-}}\mathrm{\mapsto }{\mathrm{I}}_{\mathrm{2}}\mathrm{+}\mathrm{2}\mathrm{S}{{\mathrm{O}}_{\mathrm{4}}}^{\mathrm{2}\mathrm{-}}}$

Cette réaction est lente et pratiquement totale.

Ils sont partis à $\mathrm{t}\mathrm{=}\mathrm{0}$ du même mélange : $\mathrm{50}\mathrm{m}\mathrm{l}$ d’une solution aqueuse de $\mathrm{K}\mathrm{I}$ et de concentration ${\mathrm{C}}_{\mathrm{1}}\mathrm{=}\mathrm{ }\mathrm{0}\mathrm{,}\mathrm{5}\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{.}{\mathrm{L}}^{\mathrm{-}\mathrm{1}}$ et $\mathrm{50}\mathrm{m}\mathrm{l}$ d’une solution aqueuse de $\mathrm{N}{\mathrm{a}}_{\mathrm{2}}{\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{8}}$ de concentration ${\mathrm{C}}_{\mathrm{2}}$.

Le groupe A suit l’évolution de la réaction à la température ambiante, par contre le groupe B suit l’évolution de la réaction dans un bain marie dont la température est maintenue à $\mathrm{T}\mathrm{=}\mathrm{80}\mathrm{°}\mathrm{C}$ .

À l’aide d’un protocole bien approprié qui n’est pas décrit ici les deux groupes ont tracé les deux courbes qui traduisent l’évolution de l’avancement $\mathrm{x}$ au cours du temps sur le même graphique ci-dessous :

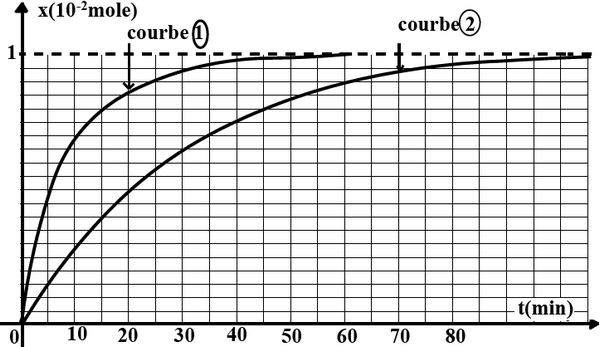
1. Identifier la courbe tracée par le groupe B .Justifier la réponse.

2. Préciser l’effet de la température sur le déroulement de la réaction chimique étudiée .Que peut-ton dire de la température ?

3. Dresser le tableau d’avancement descriptif qui décrit l’évolution de la réaction .

4. Déterminer l’avancement maximal ${\mathrm{x}}_{\mathrm{f}}$.

5. Montrer que ${\mathrm{S}}_{\mathrm{2}}{{\mathrm{O}}_{\mathrm{8}}}^{\mathrm{2}\mathrm{-}}$ est le réactif limitant. Et déduire la valeur de la concentration ${\mathrm{C}}_{\mathrm{2}}$.

6. Déterminer la composition de chaque système chimique après un quart d’heure du départ de la réaction.

7. Déterminer la vitesse de la réaction dans chaque condition à la même date $\mathrm{t}\mathrm{=}\mathrm{15}\mathrm{m}\mathrm{i}\mathrm{n}$.

IV- Exercices

4-2/ Exercice 2

On attaque 2g de limaille de zinc $\mathrm{Z}{\mathrm{n}}_{\left(s\right)}$ par un volume V =15 mL d'une solution aqueuse de chlorure d'hydrogène $\mathrm{(}{{\mathrm{H}}^{\mathrm{+}}}_{\left(aq\right)}\mathrm{+}\mathrm{C}{{\mathrm{l}}^{\mathrm{-}}}_{\left(aq\right)}\mathrm{)}$ de concentration molaire $\mathrm{C}\mathrm{=}\mathrm{0}\mathrm{,}\mathrm{12}\mathrm{ }\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{.}{\mathrm{L}}^{\mathrm{-}\mathrm{1}}$. 

On suit l'évolution du système au cours du temps en mesurant le volume de dihydrogène dégagé à température et pression constantes pour lesquelles le volume molaire ${\mathrm{V}}_{\mathrm{m}}$ des gaz est de $\mathrm{24}\mathrm{ }\mathrm{L}\mathrm{.}\mathrm{m}\mathrm{o}{\mathrm{l}}^{\mathrm{-}\mathrm{1}}$.

Les résultats obtenus sont consignés dans le tableau suivant

1. Écrire l'équation chimique qui symbolise cette réaction. ${\mathrm{H}}^{\mathrm{+}}\mathrm{/}{\mathrm{H}}_{\mathrm{2}}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{Z}{\mathrm{n}}^{\mathrm{2}\mathrm{+}}\mathrm{/}\mathrm{Z}\mathrm{n}$

2. Dresser le tableau descriptif d'évolution du système.

3. Donner l'expression de sa vitesse volumique instantanée en fonction de $\mathrm{V}\mathrm{\left(}{\mathrm{H}}_{\mathrm{2}}\mathrm{\right)}$.

4. Tracer la courbe représentant la variation de $\mathrm{V}\mathrm{\left(}{\mathrm{H}}_{\mathrm{2}}\mathrm{\right)}$ en fonction du temps.

5. Calculer la vitesse volumique de la réaction à l'instant de date $\mathrm{t}\mathrm{=}\mathrm{50}\mathrm{ }\mathrm{s}$.

IV- Exercices

4-3/ Exercice 3

Lors d'une séance de travaux pratiques, on mélange un volume ${\mathrm{V}}_{\mathrm{1}}\mathrm{ }\mathrm{=}\mathrm{ }\mathrm{10}\mathrm{ }\mathrm{m}\mathrm{L}$ de solution de peroxodisulfate de sodium $\mathrm{N}{\mathrm{a}}_{\mathrm{2}}{\mathrm{S}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{8}}$ de concentration ${\mathrm{C}}_{\mathrm{1}}\mathrm{=}\mathrm{0}\mathrm{,}\mathrm{10}\mathrm{ }\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{.}{\mathrm{L}}^{\mathrm{-}\mathrm{1}}$ avec un volume ${\mathrm{V}}_2\mathrm{ }\mathrm{=}\mathrm{ }\mathrm{90}\mathrm{ }\mathrm{m}\mathrm{L}$ de solution d'iodure de potassium $\mathrm{K}\mathrm{I}$ de concentration ${\mathrm{C}}_2\mathrm{=}\mathrm{0}\mathrm{,}\mathrm{10}\mathrm{ }\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{.}{\mathrm{L}}^{\mathrm{-}\mathrm{1}}$.

Par une méthode convenable, on détermine, à différents instants, la concentration $\left[I_2\right]$ du diiode et on trace la courbe $\left[I_2\right]=f\left(t\right)$.

1. Écrire l'équation chimique de la réaction qui modélise cette transformation, les couples rédox mis en jeu ${\mathrm{I}}_{\mathrm{2}}\mathrm{/}{\mathrm{I}}^{\mathrm{-}}$ et ${\mathrm{S}}_{\mathrm{2}}{{\mathrm{O}}_{\mathrm{8}}}^{\mathrm{2}\mathrm{-}}\mathrm{/}\mathrm{S}{{\mathrm{O}}_{\mathrm{4}}}^{\mathrm{2}\mathrm{-}}$

2. S'agit-il d'une transformation lente ou rapide?

3. Montrer que l'un des réactifs est en excès.

4. Calculer la concentration du diiode à l'état final.

5. Déduire l'avancement final ${\mathrm{x}}_{\mathrm{f}}$ de la réaction ainsi que le temps de demi-réaction.

6. Calculer la concentration finale du réactif en excès.

IV- Exercices

4-4/ Exercice 4

Dans un ballon , on verse un volume ${\mathrm{V}}_{\mathrm{A}}\mathrm{=}\mathrm{75}\mathrm{,}\mathrm{0}\mathrm{m}\mathrm{l}$ d'une solution concentrée d’acide sulfurique $(2H_3{O}^{+}+S{O_4}^{2-})$ de concentration en ions oxonium $\left[H_3{O}^{+}\right]\mathrm{=}\mathrm{0}\mathrm{,}\mathrm{4}\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{/}\mathrm{L}$  . 

À l’instant initial, on introduit une masse de $\mathrm{m}\mathrm{=}\mathrm{0}\mathrm{,}\mathrm{6}\mathrm{g}$ de zinc en poudre . 

Très rapidement, on ferme ce ballon avec un bouchon percé qui permet de relier par un tuyau le contenu du ballon avec un manomètre. 

On note, régulièrement, la valeur de la pression indiquée sur le manomètre.

Données : La masse molaire du zinc : $\mathrm{M}\left(Zn\right)\mathrm{=}\mathrm{65}\mathrm{,}\mathrm{4}\mathrm{ }\mathrm{g}\mathrm{/}\mathrm{m}\mathrm{o}\mathrm{l}$

1. Calculer ${\mathrm{n}}_{\mathrm{i}}\left(H_3{O}^{+}\right)$ la quantité de matière initiale des ions oxonium et ${\mathrm{n}}_{\mathrm{i}}\mathrm{\left(}\mathrm{Zn}\mathrm{\right)}$ la quantité de matière initiale de zinc .

2. Dresser le tableau d’avancement de cette transformation , en considérant $\mathrm{x}$ comme l’avancement de cette transformation et ${\mathrm{x}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ son avancement maximal .

3. En appliquant l’équation d’état d’un gaz parfait et en utilisant le tableau d’avancement , trouver l’ expression de l’avancement x à l’instant t en fonction de R, T, V et $\mathrm{\Delta }\mathrm{P}$ avec $\mathrm{\Delta }\mathrm{P}\mathrm{=}\mathrm{P}\left(t\right)\mathrm{-}{\mathrm{P}}_{\mathrm{0}}$ tel que ${\mathrm{P}}_{\mathrm{0}}$ la pression initiale mesuré à l’instant t=0 et $\mathrm{P}$ la pression à l’instant t .

Soit $\mathrm{\Delta }{\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\mathrm{=}{\mathrm{P}}_{\max }\mathrm{-}{\mathrm{P}}_{\mathrm{0}}$ la variation de pression maximale.

4. Montrer que : $\mathrm{x}\left(t\right)\mathrm{=}{\mathrm{x}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\frac{\mathrm{\Delta }\mathrm{P}\left(t\right)}{\mathrm{\Delta }{\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}$

Cette expérience nous a permis de tracer la courbe dans la figure ci-dessous qui représente la variation de $\mathrm{\Delta P}\mathrm{\left(}\mathrm{t}\mathrm{\right)}$ en fonction du temps t.

5. Déterminer graphiquement la valeur du temps de demi-réaction ${\mathrm{t}}_{\mathrm{1}\mathrm{/}\mathrm{2}}$.