Séance 10 - Dipôle RC

Sommaire

I- Le condensateur

1-1/ Définition

1-2/ Charge d’un condensateur

1-3/ Décharge d’un condensateur

1-4/ Relation entre charge q(t) et intensité du courant i(t)

1-5/ Relation entre charge q(t) et tension U(t) (Capacité du condensateur)

1-6/ Relation entre i, C et U

II- L’association des condensateurs

2-1/ Association en série

2-2/ Association en parallèle

III- Dipôle RC

3-1/ définition

3-2/ réponse d'un Dipôle RC à un échelon montant de tension (Charge du condensateur)

3-3/ Réponse d'un Dipôle RC à un échelon descendant de tension (Décharge du condensateur)

3-4/ Charge et décharge périodiques

IV- Énergie emmagasinée dans un condensateur

V- Exercices

5-1/ Exercice 1

5-2/ Exercice 2

5-3/ Exercice 3

5-4/ Exercice 4

I- Le condensateur

1-1/ Définition

Un condensateur est un composant électrique, formé de deux armatures métalliques en face l'une de l’autre et séparées par un isolant appelé le diélectrique (air, papier, céramiques...).

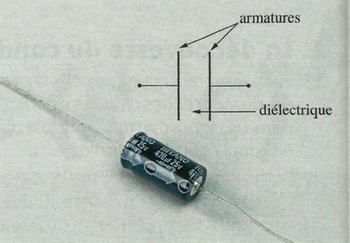
I- Le condensateur

1-2/ Charge d’un condensateur

Expérience

On utilise un générateur de tension continue de tension E et on réalise le montage suivant :

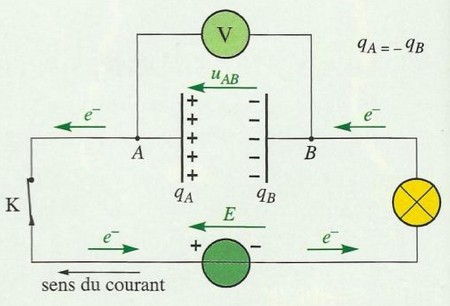
Observation

On ferme l'interrupteur K.

On observe que l'ampèremètre indique le passage d'un courant électrique durant un temps très court et que le voltmètre indique que la tension aux bornes du condensateur $U_{AB}=E$.

On dit que le condensateur est chargé et le courant électrique qui passe dans le circuit s'appelle courant de charge.

Interprétation

Le courant de charge résulte d'un déplacement des électrons de l'armature A vers l'armature B du condensateur, et à cause de l'existence du diélectrique entre les armatures, les électrons s'accumulent sur l'armature B.

L'armature A perd le même nombre d'électrons gagnés par l'armature B et condensateur devient chargé.

On appelle charge "q" du condensateur, la valeur absolue de la quantité d'électricité que porte chaque armature: $q=q_A=-q_B$

Une fois chargé, le condensateur conserve la charge électrique "q" sur ses armatures et la tension $U_{AB}=E$ entre ses bornes, même lorsqu'on le débranche.

I- Le condensateur

1-3/ Décharge d’un condensateur

Expérience

Observation

On bascule l'interrupteur K à la position (2).

Le voltmètre indique une annulation rapide de la tension aux bornes du condensateur.

Interprétation

En déplaçant l'interrupteur à la position (2) on relie les armatures entre elles.

Les électrons accumulés sur l'armature B reviennent à l'armature A et un courant de décharge apparaît dans le circuit dans le sens inverse du courant de charge.

I- Le condensateur

1-4/ Relation entre charge q(t) et intensité du courant i(t)

Par définition, l’intensité i du courant correspond au débit de charges transportées, c’est-à-dire à la charge électrique transportée par unité de temps :

$\overline{)\mathrm{i}\left(t\right)\mathrm{=}\frac{\mathrm{d}\mathrm{q}\left(t\right)}{\mathrm{d}\mathrm{t}}}$

La charge électrique q(t) est une fonction du temps dont i(t) est la dérivée.

Cette relation est valable aussi bien lors de la charge que lors de la décharge.

I- Le condensateur

1-5/ Relation entre charge q(t) et tension U(t) (Capacité du condensateur)

On réalise le montage de la figure ci-dessous en utilisant un générateur de courant (qui débite un courant électrique constant quelle que soit la tension entre ses bornes) :

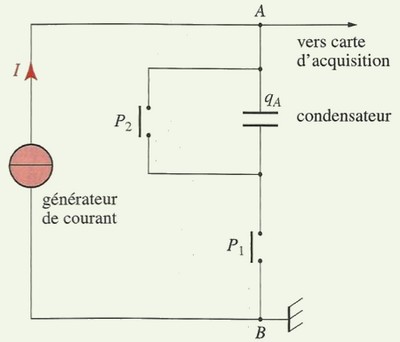
On obtient la courbe suivante :

La charge q d’un condensateur est proportionnelle à la tension U entre ses armatures : q = a x U.

Ce coefficient de proportionnalité a, toujours positif, est appelé capacité du condensateur et on le note C.

$\overline{)\mathrm{q}\left(t\right)\mathrm{=}\mathrm{C}\mathrm{.}\mathrm{U}\left(t\right)}$

La capacité C d’un condensateur dépend de :

• Surface des armatures
• son épaisseur
• nature de l’isolant
• Distance entre les armatures
• Matière de l’armature

I- Le condensateur

1-6/ Relation entre i, C et U

$\{\begin{array}{l}q=C\times U\\ i=\frac{dq}{dt}\end{array} \Rightarrow \overline{)i\left(t\right)=C\times \frac{dU\left(t\right)}{dt}}$

II- L’association des condensateurs

2-1/ Association en série

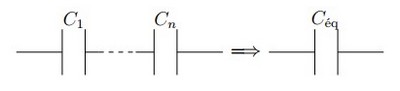
Puisque le montage est en série alors :

$$\begin{gathered} \{\begin{array}{l}U=U_1+U_2+...+U_n\\ i=i_1=i_2=...=i_n\end{array} \\ \mathrm{\Rightarrow }{\mathrm{U}}_{\mathrm{e}\mathrm{q}}\mathrm{=}\mathrm{\sum }_{}^{}{\mathrm{U}}_{\mathrm{i}} \\ \mathrm{\Rightarrow }\frac{\mathrm{q}}{{\mathrm{C}}_{\mathrm{e}\mathrm{q}}}\mathrm{=}\mathrm{\sum }_{}^{}\frac{\mathrm{q}}{{\mathrm{C}}_{\mathrm{i}}} \\ \mathrm{\Rightarrow }\overline{)\frac{\mathrm{1}}{{\mathrm{C}}_{\mathrm{e}\mathrm{q}}}\mathrm{=}\sum _{}^{}\frac{\mathrm{1}}{{\mathrm{C}}_{\mathrm{i}}}} \end{gathered}$$

II- L’association des condensateurs

2-2/ Association en parallèle

Puisque le montage est en parallèle alors :

$$\begin{gathered} \mathrm{\{}\begin{array}{l}\mathrm{U}\mathrm{=}{\mathrm{U}}_{\mathrm{1}}\mathrm{=}{\mathrm{U}}_{\mathrm{2}}\mathrm{=}\mathrm{.}\mathrm{.}\mathrm{.}\mathrm{=}{\mathrm{U}}_{\mathrm{n}}\\ \mathrm{i}\mathrm{=}{\mathrm{i}}_{\mathrm{1}}\mathrm{+}{\mathrm{i}}_{\mathrm{2}}\mathrm{+}\mathrm{.}\mathrm{.}\mathrm{.}\mathrm{+}{\mathrm{i}}_{\mathrm{n}}\end{array} \\ \mathrm{\Rightarrow }{\mathrm{q}}_{\mathrm{eq}}\mathrm{=}\sum _{}^{}{\mathrm{q}}_{\mathrm{i}} \\ \mathrm{\Rightarrow }{\mathrm{C}}_{\mathrm{eq}}\mathrm{.}\mathrm{U}\mathrm{=}\sum _{}^{}{\mathrm{C}}_{\mathrm{i}}\mathrm{.}\mathrm{U} \\ \mathrm{\Rightarrow }\overline{){\mathrm{C}}_{\mathrm{eq}}\mathrm{=}\sum _{}^{}{\mathrm{C}}_{\mathrm{i}}} \end{gathered}$$

III- Dipôle RC

3-1/ définition

Un dipôle RC est l’association en série d’un conducteur ohmique de résistance R et d’un condensateur de capacité C.

III- Dipôle RC

3-2/ réponse d'un Dipôle RC à un échelon montant de tension (Charge du condensateur)

Échelon de tension

On dit qu'un dipôle est soumis à un échelon montant de tension, si la tension entre ses bornes varie instantanément d'une valeur nulle à une valeur constante E.

Étude expérimentale

Soit le circuit suivant :

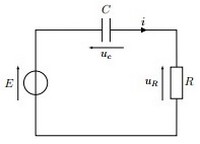
Sur l’oscilloscope on obtient la courbe qui comporte deux régimes :

1. Régime transitoire : dans lequel la tension aux bornes du condensateur croît depuis la valeur 0.
2. Régime permanent : dans lequel la tension reste pratiquement constante. Lorsque $t\to \infty$, $u_c$ tend vers E.

III- Dipôle RC

3-2/ réponse d'un Dipôle RC à un échelon montant de tension (Charge du condensateur)

Équation différentielle

D’après la loi d’additivité des tensions on a :

$$\begin{gathered} E=u_c+u_R \\ E=u_c+R.i \\ E=u_c+R\frac{dq}{dt} \\ E=u_c+RC\frac{d{u}_c}{dt} \end{gathered}$$

Donc on en déduit l’équation suivante :

$\overline{){\mathrm{u}}_{\mathrm{c}}\mathrm{+}\mathrm{\tau }\frac{\mathrm{d}{\mathrm{u}}_{\mathrm{c}}}{\mathrm{d}\mathrm{t}}\mathrm{=}\mathrm{E}}$

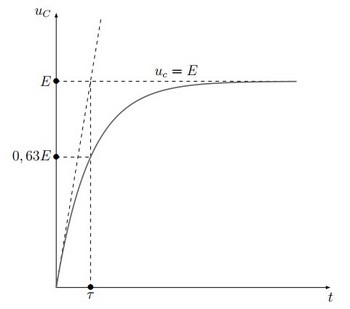
$\tau =\mathrm{RC}$ : Constante du temps

C’est une équation différentielle d’inconnue uc, dont la solution s’écrit sous la forme suivante :

$\overline{){\mathrm{u}}_{\mathrm{c}}\left(t\right)\mathrm{=}\mathrm{A}\mathrm{.}{\mathrm{e}}^{\mathrm{-}\mathrm{\lambda }\mathrm{t}}\mathrm{+}\mathrm{B}}$

$\lambda =\frac{1}{RC}=\frac{1}{\tau } ; B=E ; A=-E$

Donc la solution de l'équation différentielle est :

$\overline{){\mathrm{u}}_{\mathrm{c}}\mathrm{\left(}\mathrm{t}\mathrm{\right)}\mathrm{=}\mathrm{E}\mathrm{.}\mathrm{(}\mathrm{1}\mathrm{-}{\mathrm{e}}^{\mathrm{-}\frac{\mathrm{t}}{\mathrm{\tau }}}\mathrm{)}}$

III- Dipôle RC

3-2/ réponse d'un Dipôle RC à un échelon montant de tension (Charge du condensateur)

Détermination graphique de la valeur de $\tau$

 $$\begin{gathered} t=\tau \\ \Rightarrow u_c=E\left(1-e^{-1}\right)\approx 0,63E \end{gathered}$$

III- Dipôle RC

3-2/ réponse d'un Dipôle RC à un échelon montant de tension (Charge du condensateur)

Expression de l'intensité du courant dans le circuit

$$\begin{gathered} i\left(t\right)=C\frac{d{u}_c}{dt} \\ i\left(t\right)=C\frac{d}{dt}\left(E\left(1-e^{-\frac{t}{\tau }}\right)\right) \\ i\left(t\right)=C\frac{E}{\tau }{e}^{-\frac{t}{\tau }} \\ i\left(t\right)=\frac{E}{R}{e}^{-\frac{t}{\tau }} \\ \overline{)i\left(t\right)=I_0{e}^{-\frac{t}{\tau }} \left(I_0=\frac{E}{R}\right)} \end{gathered}$$

III- Dipôle RC

3-3/ Réponse d'un Dipôle RC à un échelon descendant de tension (Décharge du condensateur)

Soit le circuit suivant :

Sur un oscilloscope on obtient la courbe qui comporte deux régimes :

• Régime transitoire : dans lequel la tension uc décroît depuis sa valeur initiale.
• Régime permanent : dans lequel la tension uc reste pratiquement nulle, lorsque $t\to \infty$ alors $u_c\to \infty$

III- Dipôle RC

3-3/ Réponse d'un Dipôle RC à un échelon descendant de tension (Décharge du condensateur)

Équation différentielle

$\overline{){\mathrm{u}}_{\mathrm{c}}\mathrm{+}\mathrm{\tau }\frac{\mathrm{d}{\mathrm{u}}_{\mathrm{c}}}{\mathrm{d}\mathrm{t}}\mathrm{=}\mathrm{0}}$

C’est une équation différentielle d’inconnue $u_c$, dont la solution s’écrit sous la forme suivante :

$\overline{){\mathrm{u}}_{\mathrm{c}}\mathrm{\left(}\mathrm{t}\mathrm{\right)}\mathrm{=}\mathrm{E}\mathrm{.}{\mathrm{e}}^{\mathrm{-}\frac{\mathrm{t}}{\mathrm{\tau }}}}$

Détermination graphique de la valeur de $\tau$

$$\begin{gathered} t=\tau \\ \Rightarrow u_c=E.e^{-1}\approx 0,37E \end{gathered}$$

III- Dipôle RC

3-3/ Réponse d'un Dipôle RC à un échelon descendant de tension (Décharge du condensateur)

Expression de l'intensité du courant dans le circuit

$$\begin{gathered} i\left(t\right)=C\frac{d{u}_c}{dt} \\ i\left(t\right)=C\frac{d}{dt}\left(E.e^{-\frac{t}{\tau }}\right) \\ i\left(t\right)=-C.\frac{E}{\tau }{e}^{-\frac{t}{\tau }} \\ i\left(t\right)=-\frac{E}{R}{e}^{-\frac{t}{\tau }} \\ \overline{)i\left(t\right)=-I_0{e}^{-\frac{t}{\tau }} \left(I_0=\frac{E}{R}\right)} \end{gathered}$$

III- Dipôle RC

3-4/ Charge et décharge périodiques

Courbe de la tension

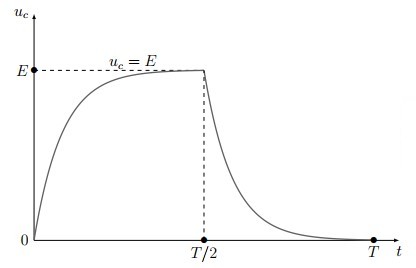
Courbe du courant

IV- Énergie emmagasinée dans un condensateur

Soit $E_c$ l'énergie électrique emmagasinée dans un condensateur.

$\overline{){\mathrm{E}}_{\mathrm{c}}\mathrm{=}\frac{\mathrm{1}}{\mathrm{2}}\mathrm{.}\mathrm{C}\mathrm{.}{{\mathrm{u}}_{\mathrm{c}}}^{\mathrm{2}}\mathrm{=}\frac{\mathrm{1}}{\mathrm{2}}\mathrm{.}\frac{{\mathrm{q}}^{\mathrm{2}}}{\mathrm{C}}}$

V- Exercices

5-1/ Exercice 1

Un condensateur initialement déchargé, de capacité $C$, est branché en série avec un conducteur ohmique de résistance $R=10K\Omega$ :

La tension aux bornes du générateur est $E = 5,00V$. À l’instant t = 0, on ferme le circuit. La tension $u_C\left(t\right)$, enregistrée au cours de la charge, est représentée graphiquement :

1. Établir l’équation différentielle de la tension uc aux bornes du condensateur lors de se charge.

La solution de l’équation différentielle est la suivante : $u_C\left(t\right)=A\left(1-e^{-\alpha .t}\right)$

2. Déterminer $A$ et $\alpha$ en fonction de $E$, $R$ et $C$

3. Exprimer la constante de temps $\tau$ en fonction de $\alpha$, calculer $u_C$ pour $t=\tau$

4. Déterminer la valeur numérique de $\tau$ à l’aide de graphique (préciser la méthodes utilisé)

5. Déterminer la capacité $C$ de condensateur

V- Exercices

5-2/ Exercice 2

À l’aide d’un générateur de tension idéale, de deux résistors et d’un condensateur, on réalise le montage représenté par le figure ci-dessous :

À l’aide d’un oscilloscope, on enregistre la charge d’un condensateur de capacité C à travers le résistor de résistance $R_1=20\Omega$ puis sa décharge à travers le résistor de résistance $R_2$ on obtient le digramme suivant :

1. Expliquer comment doit-on procéder pour obtenir l’oscillogramme précédent.

2. Donner la valeur de la tension du générateur U.

3. Déterminer la valeur de C et de $R_2$.

4. $U_c\left(t\right)$ présente-t-elle une discontinuité en passant de la charge à la décharge ?

5. Qu’en est-il de l’intensité du courant i(t) qui parcourt le circuit ?

V- Exercices

5-3/ Exercice 3

Le montage du document ci-dessous permet, lorsque le commutateur est en position 1, de charger simultanément deux condensateurs de capacités $C_1$ et $C_2$ :

Les deux conducteurs ohmiques ont la même résistance $R=2,2K\Omega$

Un système d'acquisition permet d'enregistrer l’évolution des tensions $u_{c_1}\left(t\right)$ et $u_{c_2}\left(t\right)$ :

1. Les deux condensateurs sont-ils chargés à la fin de l'acquisition ?

2. En déduire la valeur de la tension aux bornes du générateur.

La tension $u_c\left(t\right)$ aux bornes d'un condensateur lors de la charge est : $u_c\left(t\right)=E.\left(1-e^{-\frac{t}{\tau }}\right)$  avec E la tension aux bornes du générateur.

3. Quelle est la valeur de la tension $u_c\left(\tau \right)$ ?

4. Déterminer les constantes de temps ${\tau }_1$ et ${\tau }_2$ de chacun des dipôles $\left(R,C_1\right)$ et $\left(R,C_2\right)$ .

5. Quelles sont les capacités $C_1$ et $C_2$ des condensateurs ?

6. Plus la capacité d'un condensateur est grande, plus il se charge rapidement : Cette proposition est-elle correcte ?

V- Exercices

5-4/ Exercice 4

On considère le circuit électrique suivant qui est constitué par un générateur idéal de courant électrique qui débite un courant d’intensité I=100A, un condensateur gigantesque de capacité très grand C=1800F est initialement déchargé, un conducteur ohmique de résistance R=2Ω et un interrupteur K à deux position (1) et (2) (Doc 1).

À la date t = 0, l’interrupteur est basculé en position 1.

Le condensateur se charge et à l’aide d’un dispositif informatisé on obtient la courbe représentée au (Doc 2) :

1. Déterminer la date $t_1$ où la tension $u_c$ peut prendre la valeur $U_1=2V$ .

2. Calculer l’énergie électrique $E_e$ emmagasinée dans le condensateur à l’instant $t_1$.

À l’instant $t=t_1$ on bascule l’interrupteur K en position 2, le condensateur se décharge à travers le conducteur ohmique jusqu’à l’instant $t_2$ auquel $U_2=1,5V$.

L’équation de la tension $u_c$ en fonction de t est :

$u_c\left(t\right)=A+B.e^{\left(-\frac{\left(t-t_1\right)}{\tau }\right)}$

3. Déterminer A,B et $\tau$.

4. Calculer la date $t_2$ où la tension prend la valeur $U_2$

On suppose que la décharge du condensateur se fait sans perte d’énergie .

5. Calculer l’énergie dissipée par effet Joule $E_R$ dans le conducteur ohmique R entre les instants $t_1$ et $t_2$.

6. En déduire la puissance moyenne ${\mathcal{P}}_R$ dissipée par effet Joule dans le conducteur ohmique entre les instants $t_1$ et $t_2$.