Physique et Chimie : 2ème Année Bac
Séance 6 (Décroissance radioactive)
Professeur : Mr El GOUFIFA Jihad
Sommaire
I- Le noyau atomique
1-1/ Le noyau
1-2/ Représentation symbolique du noyau atomique
1-3/ Le nucléide
1-4/ Les isotopes
1-5/ Densité de la matière nucléaire
II- Noyau et radioactivité
2-1/ Diagramme de stabilité (N,Z) (Diagramme de Segré)
2-2/ Qu'est-ce que la radioactivité ?
2-3/ Propriétés de la radioactivité
2-4/ Loi de conservation de Soddy
III- Différents types de d’émissions radioactives
3-1/ Radioactivité α
3-2/ Radioactivité β-
3-3/ Radioactivité β+
3-4/ Radioactivité γ
IV- Familles radioactives
V- Décroissance radioactive
5-1/ Constante de désintégration
5-2/ Loi de décroissance radioactive
5-3/ Constante du temps
5-4/ Temps de demi vie
5-5/ Activité d’un échantillon radioactif
VI- Application de la radioactivité à la datation
6-1/ Principe
6-2/ Datation au carbone 14
VII- Comment se protéger de chaque type de rayonnement ?
IIX- Exercices
8-1/ Exercice 1
8-2/ Exercice 2
8-3/ Exercice 3
8-4/ Exercice 4
I- Le noyau atomique
1-1/ Le noyau
Le noyau atomique est composé de protons et de neutrons, ces constituants du noyau s'appellent les nucléons.
Le proton a une charge positive appelée charge élémentaire qp=+e=+1,6.10-19C, sa masse est mp=1,6726.10-27Kg
Le neutron est électriquement neutre (il n'a pas de charge électrique) qn=0C, sa masse est mn=1,6750.10-27Kg
1-2/ Représentation symbolique du noyau atomique
Le noyau atomique d'un élément chimique est représenté par le symbole :
XAZ
- X : symbole de l’élément chimique.
- A : nombre de masse (nombre de nucléons).
- Z : numéro atomique (nombre de protons).
- N=A-Z : nombre de neutrons.
1-3/ Le nucléide
Dans la physique atomique, un nucléide est l’ensemble des noyaux ayant le même nombre de nucléons A et le même nombre de protons Z.
1-4/ Les isotopes
Les isotopes d’un élément chimique sont les nucléides d'un même élément chimique qui ont le même numéro atomique Z, mais ils diffèrent par leur nombre de masse A (ils n'ont pas le même nombre de neutrons).
Exemples
C126 et C146 sont deux isotopes de l’élément carbone
U23592 et U23892 sont deux isotopes de l’élément uranium.
1-5/ Densité de la matière nucléaire
Le noyau atomique a une forme sphérique dont le rayon r varie avec la variation du nombre de masse A selon la relation suivante:
r=r0A1/3 (r=1,2.10-15m)
La masse approchée d'un nucléon est : mn≈1,7.10-27Kg
La valeur approchée de la masse volumique du noyau atomique : ρ=MV=mn×A43π.r3≈2.1017Kg/m3=2.108tonnes/cm3
La masse de 1cm3 de la matière nucléaire est 200 millions tonnes, par conséquence la matière nucléaire est extrêmement dense.
II- Noyau et radioactivité
2-1/ Diagramme de stabilité (N,Z) (Diagramme de Segré)
Certains noyaux conservent toujours la même structure, on dit que ses noyaux sont stables.
Et il y a des noyaux qui se transforment spontanément à d'autres noyaux après l'émission de rayonnement, on dit que ses noyaux sont instables ou noyaux radioactifs.
Le diagramme Segré montre l’emplacement des noyaux stables et des noyaux radioactifs, de sorte que chaque noyau est représenté par un petit carré d’abscisse Z (le nombre de protons) et d’ordonnée N (le nombre de neutrons).
La zone centrale noire s'appelle la vallée de stabilité et comprend les noyaux stables.
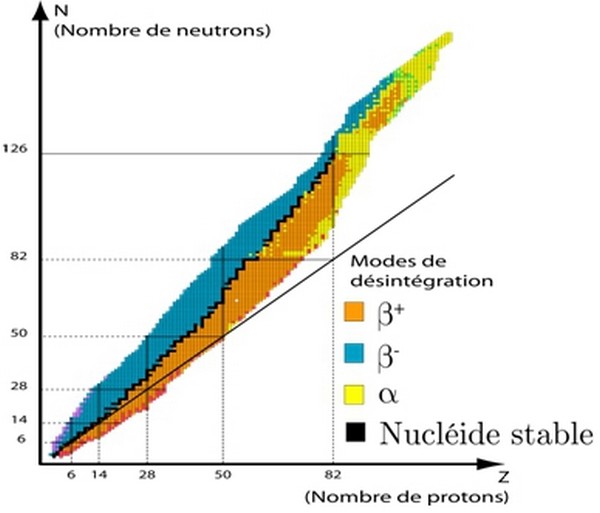
Différents isotopes du même élément chimique se trouvent sur la même droite parallèle à l'axe des ordonnées.
- Pour les nucléides de Z < 20 : la vallée de stabilité se situe au voisinage du premier médiateur (Z=N), c-à-d que les nucléides légers stables possèdent autant de protons que de neutrons.
- Pour les nucléides de Z > 20 : la vallée de stabilité se déplace au-dessus du premier médiateur quand la valeur de Z augmente C-à-d N > Z .
Donc la stabilité du noyau n’est assurée que s’il contient plus de neutrons que de protons.
II- Noyau et radioactivité
2-2/ Qu'est-ce que la radioactivité ?
En dehors de la vallée de stabilité, les noyaux instables sont dits radioactifs. Chaque noyau va se transformer en noyau stable en une ou plusieurs désintégration(s) spontanée(s).
La radioactivité est une désintégration naturelle d’un noyau radioactif à un noyau fils plus stable avec émission d’une particule.
Elle s'exprime par l’équation suivante :
XA1Z1 → YA2Z2 + PA3Z3
- X : Symbole du noyau père.
- Y : Symbole du noyau fils.
- P : Symbole de la particule émise.
2-3/ Propriétés de la radioactivité
La radioactivité est :
- Aléatoire : on ne peut pas prédire l’instant exact où un noyau va se désintégrer.
- Spontanée : la désintégration se fait sans intervention extérieure.
- Inévitable : le noyau radioactif sera désintégrer tôt ou tard, rien ne peut l’empêcher.
- Ne dépend pas des facteurs extérieurs comme la pression, la chaleur, …
- Ne dépend pas de liaisons chimiques formées par l'atome qui contient le noyau radioactif.
2-4/ Loi de conservation de Soddy
Lors des transformations nucléaires, il y a conservation du nombre de charge Z et du nombre de nucléons A.
Exemple
U23892 → Th23490 + He42
III- Différents types de d’émissions radioactives
3-1/ Radioactivité α
La radioactivité α correspond à l’émission de noyaux d’hélium H42e (particules α) par certains noyaux.
La radioactivité α concerne les noyaux présentant un excès de nucléons et appelés « noyaux lourds » (A > 200).
Équation générale : XAZ→YA-4Z-2+He42
Exemple : U23892→Th23490+He42
3-2/ Radioactivité β-
La radioactivité β- correspond à l’émission d’électrons (appelés rayons, ou particules ) par certains noyaux.
Ce type de radioactivité concerne les noyaux présentant un excès de neutrons.
Équation générale : XAZ→YAZ+1+e0-1
Exemple : C146→N147+e0-1
3-3/ Radioactivité β+
La radioactivité β+correspond à l’émission de positrons (e0+1) par certains noyaux.
La radioactivité β+concerne les noyaux présentant un excès de protons
Équation générale : XAZ→YAZ-1+e0+1
Exemple : P30 15→Si3014+e0+1
3-4/ Radioactivité γ
Le rayonnement γ est des ondes électromagnétiques de très grande énergie.
Lors des désintégrations α et β- et β+, le noyau fils est généralement produit dans un état excité (il possède un excédent d’énergie par rapport à son état fondamental).
Ce noyau libère un rayonnement γ selon l’équation suivante :
YAZ*→YAZ+γ
- YAZ* : noyau fils dans l’état excité.
- YAZ : noyau fils dans l’état fondamental.
Exemple :
- N167→O168*+e0-1 : radioactivité β-.
- O168*→O168+γ : émission de rayonnement γ.
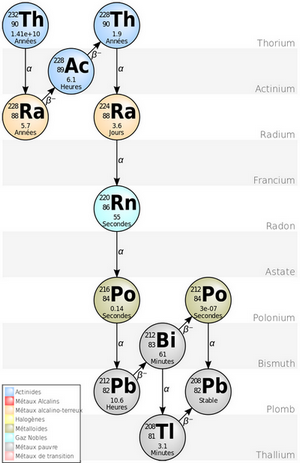
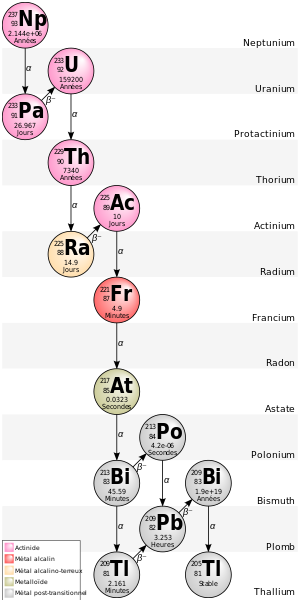
IV- Familles radioactives
La radioactivité entraîne la transformation d’un nucléide en un autre nucléide. Si ce dernier est lui-même radioactif, il se transforme à son tour, et ainsi de suite jusqu’à ce que le nucléide obtenu ne soit plus radioactif.
L’ensemble des nucléides obtenus à partir d’un même noyau père est appelé famille radioactive.
Il existe 4 familles radioactives provenant des noyaux suivants :
T23290h ; N23793p ; U23592 ; U23892
Exemple
U23892 radioactif se désintègre par une série d’émissions α et β pour aboutir à l’isotope stable non radioactif P20682b
U23892→P20682b+xα+γβ-
|
|
|
V- Décroissance radioactive
5-1/ Constante de désintégration
Soit :
N0: le nombre de noyaux présents à t = 0,
N(t): le nombre de noyaux présents à la date t.
Pendant une durée dt très brève, un certain nombre de noyaux radioactifs se sont désintégrés (disparu).
Soit N(t)+ dN(t) le nombre de noyaux radioactifs non désintégrés (Reste) à la date t+dt (avec dN(t)<0 car N diminue).
La variation du nombre moyen de noyaux désintégrés pendant la durée dt est:
Nt+dt-Nt=(N(t)+dN(t))-N(t)=dN(t)
Cette variation du nombre de noyaux désintégrés est négative et proportionnel au nombre de noyaux N présents à l’instant t et la durée dt.
On traduit cela par la relation dN(t)=-λ.N(t).dt
λ est la constante radioactive, elle dépend de la nature du noyau radioactif, c’est la proportion de noyaux qui se désintègre par unité de temps.
V- Décroissance radioactive
5-2/ Loi de décroissance radioactive
dN(t)=-λ.N(t).dt
⇒dN(t)dt+λ.N(t)=0
La solution de l’équation différentielle est La loi de décroissance radioactive qui s’écrit :
N(t)=N0.e-λ.t

V- Décroissance radioactive
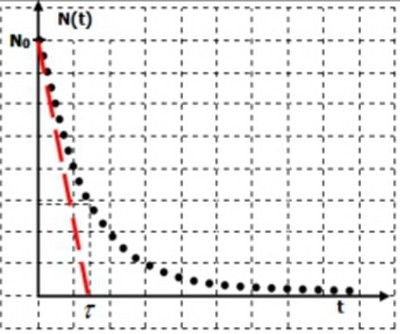
5-3/ Constante du temps
La constante de temps τ=1λ est un temps qui caractérise la substance radioactive:
V- Décroissance radioactive
5-4/ Temps de demi vie
La demi-vie d’un nucléide radioactif t1/2 est la durée au bout de laquelle la moitié des nucléides radioactifs initialement présent dans l’échantillon se sont désintégrés :
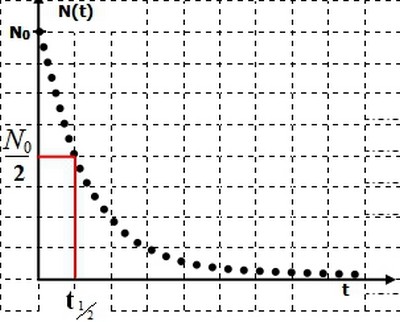
V- Décroissance radioactive
5-5/ Activité d’un échantillon radioactif
L’activité a(t) d’une source contenant N noyaux radioactifs à la date t est égale au nombre de noyaux qui se désintègrent chaque seconde.
a(t)=-dN(t)dt
L’activité se mesure en becquerel Bq, (un becquerel correspond à une désintégration par seconde).
C’est une unité très petite, aussi utilise-t-on souvent des multiples : 1MBq=106Bq
Autre unité : Curie: 1Ci=3,7.1010 Bq
L'appareil de mesure de l'activité est appelé: Appareil de Geiger.
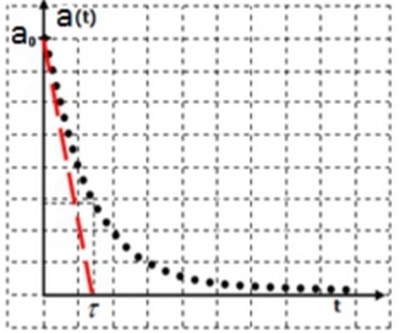
a(t)=a0.e-λ.t
VI- Application de la radioactivité à la datation
6-1/ Principe
Pour les objets issus du monde vivant l’échange dynamique entre certains organismes vivants et leur milieu extérieur (ex : le carbone 14, le potassium 40 …) maintenant constant le nombre de noyaux radioactifs dans l’organisme.
À leur mort, les échanges n’ont plus lieu et on observe une décroissance qui suit la loi exponentielle.
Remarque
Il faut tout d’abord estimer l’âge de l’échantillon à dater, pour choisir un élément radioactive dont la demi-vie est en rapport avec cet âge. Car au bout de 10×t1/2, on considère que les noyaux radioactifs sont tous désintégrés.
VI- Application de la radioactivité à la datation
6-2/ Datation au carbone 14
Isotope radioactif du carbone, le «carbone 14» noté C14 est formé continuellement dans la haute atmosphère par réaction nucléaire des neutrons cosmiques avec des noyaux d’azote.
La proportion de carbone 14 par rapport au carbone 12 est identique dans les tissus vivants (échange de carbone par respiration, avec le milieu extérieur ...)
- Pendant toute leur vie, la proportion de carbone 14 reste constante.
- A leur mort, la quantité de carbone 14 décroît par radioactivité β-.
Il est alors possible de déterminer la date de la mort en mesurant la quantité de carbone 14 restant dans l’échantillon à étudier et en le comparant à la quantité de carbone 14 présent dans un échantillon de même nature, mais vivant.
Donc l’âge :
t=1λ.ln(amortavivant)=t12ln(2).ln(amortavivant)
VII- Comment se protéger de chaque type de rayonnement ?
Les rayons alpha, très peu pénétrants, sont arrêtés par une feuille de papier ou par les couches superficielles de la peau.
Les rayons bêta, moyennement pénétrants, peuvent traverser les couches superficielles de la peau mais sont arrêtés par quelques millimètres de métal.
Les rayons gamma sont très énergétiques et donc très pénétrants: pour arrêter certains d'entre eux, plusieurs dizaines de centimètres de plomb ou plusieurs mètres de béton sont nécessaires.
IIX- Exercices
8-1/ Exercice 1
Le carbone (Z = 6) possède, entre autres, deux isotopes de nombre de masse 12 et 14.
- Donner la composition de chacun des noyaux.
La réaction d'un neutron sur un noyau d'azote N147 donne naissance à du carbone 14 et à une autre particule X.
- Écrire l'équation de cette réaction nucléaire en rappelant les lois de conservation.
- Identifier la particule X.
Le carbone 14 est radioactif β- de demi-vie t1/2 = 5570 ans.
- Écrire l'équation de la réaction de désintégration du carbone 14 en précisant la nature de la particule β- et en identifiant le noyau fils.
On appelle N le nombre de noyaux non désintégrés à l’instant t, N0 étant le nombre de noyaux initial, à l’instant t = 0.
- Donner l’expression littérale de la loi de décroissance radioactive.
- Donner la définition de demi-vie d’un élément radioactif. Exprimer la de demi-vie en fonction de λ la constante radioactive.
Dans un échantillon de bois ancien, mort, on constate que la teneur en carbone 14 est 8 fois plus faible que dans un échantillon de bois vivant de même masse.
- Déterminer l’âge de ce morceau de bois.
IIX- Exercices
8-2/ Exercice 2
L'iode est indispensable à l'organisme humain, il participe à la synthèse des hormones thyroïdiennes.
L'assimilation de cet iode 127 non radioactif se fait sous forme d'ions iodure dans la glande thyroïde.
Lors des accidents nucléaires, il y a émission dans l'atmosphère d'iode 131, radioactif β- de demi-vie t1/2=8,1 jours.
Lors de sa désintégration l'iode 131 donne du Xénon (Xe).
- Écrire l'équation de désintégration de l'iode 131.
La population française vivant dans les environs des centrales nucléaire a reçu des comprimés d'iode 127 (sous forme d'iodure de potassium) à prendre en cas d'accident nucléaire.
- Justifier cette mesure.
L'iode 131 est aussi utilisé en médecine, par exemple pour l'examen par scintigraphie des glandes surrénales.
- Déterminer l'activité A1 de m=1,0g d'iode 131.
- Sachant que pour cet examen il faut une solution d'iode 131 d'activité A0=37MBq. Quelle est alors la masse m' d'iode 131 injectée au patient ?
- Tracer la courbe de décroissance de l'activité du produit injecté au cours du temps et déterminer graphiquement la date t où l'activité sera divisée par 10.
Données :
- Iode 131 : I13153 ; M (iode 131) = 131g/mol
- Constante d'Avogadro : NA = 6,02.1023 mol-1
IIX- Exercices
8-3/ Exercice 3
Lorsque, dans la haute atmosphère, un neutron appartenant au rayonnement cosmique rencontre un noyau d’azote N147, il donne naissance à du carbone 14, isotope de carbone C126.
- Écrire l’équation de la réaction en précisant la nature de la particule apparue avec le carbone 14 .
Le noyau de carbone 14 se désintègre en émettant un rayonnement β-.
- Écrire le bilan de cette réaction nucléaire .
Des végétaux absorbent le dioxyde de carbone de l’atmosphère provenant indifféremment du carbone 14 et de carbone 12.
La proportion de ces deux isotopes est la même dans les végétaux vivants et dans l’atmosphère.
Mais lorsque la plante meurt, elle cesse d’absorber le dioxyde de carbone ; le carbone 14 qu’elle contient se désintègre alors, sans être renouvelé, avec une demi-vie t1/2 = 5570 ans .
- Quelle sera l’activité d’un échantillon de végétal au bout d’une durée t=n.t1/2 après sa mort ?
Donnée : en.ln2=2n
On a comparé l’activité a1 d’un échantillon de bois trouvé dans une tombe égyptienne en 1998 avec l’activité a2 d’un échantillon de référence dont l’activité était a0 en 1985.
Le rapport est a2a1=1,85
- Calculer l’ordre de grandeur de la date de la coupe du bois trouvé dans la tombe.
IIX- Exercices
8-4/ Exercice 4
L’air contient l’isotope du radon 222 en quantité plus ou moins importante.
Ce gaz radioactif naturel provient des roches qui contenaient de l’uranium et du radium.
À un instant pris comme origine du temps (t=0), l’activité d’un échantillon de radon 222 est A0.
À une date ultérieure t, La mesure de l’activité A de cet échantillon à différents instants a permis de tracer la courbe de la figure ci-dessous représentant les variations de Ln(A) en fonction du temps t où Ln désigne le logarithme népérien et A est l’activité de l’échantillon à l’instant t, exprimée en Bq. cette activité devient A.
- Donner l’expression de la loi de décroissance radioactive en fonction de A.
- Déduire graphiquement la valeur de la période radioactive du radon 222.
- Déterminer l’activité initiale de l’échantillon radioactive à t=0.
- Calculer le nombre N de noyau de radon 222 désintégrés pendant 50 jours.