Séance 3 - Propagation d'une onde lumineuse

Sommaire

I- La lumière, un phénomène ondulatoire

1-1/ Diffraction de la lumière

1-2/ La lumière est une onde

II- Caractéristiques d'une onde lumineuse

2-1/ Lumière monochromatique et polychromatique

2-2/ Célérité de la lumière

2-3/ Indice de réfraction

2-4/ Fréquence et longueur d'onde

2-5/ Domaine des radiations lumineuses

III- Diffraction d’une onde lumineuse monochromatique

3-1/ Expérience

3-2/ Écart angulaire

IV- Phénomène de dispersion de la lumière par un prisme

4-1/ Relations caractéristiques du prisme

4-2/ Dispersion de la lumière

4-3/ Interprétation de la dispersion

V- Exercices

5-1/ Exercice 1

5-2/ Exercice 2

5-3/ Exercice 3

5-4/ Exercice 4

I- La lumière, un phénomène ondulatoire

1-1/ Diffraction de la lumière

Expérience

La lumière se propage en ligne droite dans un milieu transparent homogène.

Lorsqu’un rayon lumineux rencontre une fente fine, la lumière ne se propage plus en une ligne droite, elle est diffractée par la fente dans un plan perpendiculaire à son axe. On obtient des tâches sur l’écran.

Définition de la diffraction

La diffraction est le phénomène au cours duquel une onde qui traverse une petite ouverture ou rencontre un petit objet change de direction sans modification des propriétés de l’onde (la fréquence, la période et la longueur d’onde).

Ce phénomène est d’autant plus important lorsque la fente a est faible.

De cette expérience on peut déduire que la lumière a un aspect ondulatoire, c’est une onde électromagnétique qui se propage dans les milieux transparents et le vide.

1-2/ La lumière est une onde

La lumière n’a pas besoin d’un milieu matériel pour se propager.

La lumière ne se propage pas dans les milieux opaques (bois, pierre...).

La lumière est une onde électromagnétique (correspond à la propagation simultanée d’un champ électrique et magnétique ) qui se propage dans le vide et dans les milieux transparents (air, eau, verre...).

II- Caractéristiques d'une onde lumineuse

2-1/ Lumière monochromatique et polychromatique

Onde lumineuse monochromatique

La lumière monochromatique est celle qui ne peut pas être décomposée par le prisme, à titre d’exemple le rayonnement laser.

Une onde lumineuse monochromatique est une onde progressive sinusoïdale caractérisée par :

• Périodicité temporelle : caractérisée par aa fréquence $\nu$ ou la période $\mathrm{T}$ imposées par la source de l’onde $\overline{)\mathrm{\nu }\mathrm{=}\frac{\mathrm{1}}{\mathrm{T}}}$.
• Périodicité spatiale : caractérisée par la longueur d'onde $\mathrm{\lambda }$ et la vitesse $\mathrm{V}$ qui dépend du milieu dans lequel l’onde se propage $\overline{)\mathrm{V}\mathrm{=}\frac{\mathrm{\lambda }}{\mathrm{T}}\mathrm{=}\mathrm{\lambda }\mathrm{.}\mathrm{\nu }}$.

Onde lumineuse polychromatique

L'onde lumineuse polychromatique est composée d’un ensemble de lumières monochromatiques de fréquences différentes (composée de plusieurs radiations donc de plusieurs couleurs).

Exemple: Lumière blanche

II- Caractéristiques d'une onde lumineuse

2-2/ Célérité de la lumière

Dans le vide et pratiquement dans l’air, toutes les radiations lumineuses se propagent avec la même célérité $\mathrm{C}\mathrm{ }\mathrm{=}\mathrm{ }\mathrm{3}\mathrm{,}\mathrm{00}\mathrm{.}{\mathrm{10}}^{\mathrm{8}}\mathrm{ }\mathrm{m}\mathrm{/}\mathrm{s}$, quelque soit leur fréquence.

Dans les milieux transparents (comme le verre ou l’eau...) la célérité $\mathrm{\nu }$ de la lumière est inférieure à c et différente d’un milieu à l’autre

Exemples :

• ${\mathrm{\nu }}_{\mathrm{e}\mathrm{a}\mathrm{u}}\mathrm{ }\mathrm{=}\mathrm{ }\mathrm{2}\mathrm{,}\mathrm{25}\mathrm{.}{\mathrm{10}}^{\mathrm{8}}\mathrm{ }\mathrm{m}\mathrm{/}\mathrm{s}$
• ${\mathrm{\nu }}_{\mathrm{verre}}\mathrm{ }\mathrm{=}\mathrm{ }\mathrm{2}\mathrm{.}{\mathrm{10}}^{\mathrm{8}}\mathrm{ }\mathrm{m}\mathrm{/}\mathrm{s}$

2-3/ Indice de réfraction

L’indice de réfraction d’un milieu est le rapport des célérités : $\overline{)\mathrm{n}\mathrm{=}\frac{\mathrm{C}}{\mathrm{\nu }}}$

Exemples :

• $\overline{){\mathrm{n}}_{\mathrm{eau}}\mathrm{ }\mathrm{=}\frac{\mathrm{c}}{{\mathrm{\nu }}_{\mathrm{eau}}}\mathrm{ }\mathrm{=}\mathrm{ }\frac{\mathrm{3}\mathrm{.}{\mathrm{10}}^{\mathrm{8}}}{\mathrm{2}\mathrm{,}\mathrm{25}\mathrm{.}{\mathrm{10}}^{\mathrm{8}}}\mathrm{=}\mathrm{1}\mathrm{,}\mathrm{33}}$
• $\overline{){\mathrm{n}}_{\mathrm{verre}}\mathrm{ }\mathrm{=}\frac{\mathrm{c}}{{\mathrm{\nu }}_{\mathrm{verre}}}\mathrm{ }\mathrm{=}\mathrm{ }\frac{\mathrm{3}\mathrm{.}{\mathrm{10}}^{\mathrm{8}}}{\mathrm{2}\mathrm{.}{\mathrm{10}}^{\mathrm{8}}}\mathrm{=}\mathrm{1}\mathrm{,}\mathrm{5}}$

II- Caractéristiques d'une onde lumineuse

2-4/ Fréquence et longueur d'onde

Une onde lumineuse (radiation lumineuse) est une onde progressives sinusoïdale caractérisée par sa longueur d’onde dans le vide $\mathrm{\lambda }$ (exprimée en mètres).

Celle-ci est reliée à la période de l’onde T ou à sa fréquence ν par l’intermédiaire de la célérité :

$\overline{)\mathrm{C}\mathrm{=}\frac{{\mathrm{\lambda }}_{\mathrm{0}}}{\mathrm{T}}\mathrm{=}{\mathrm{\lambda }}_{\mathrm{0}}\mathrm{.}\mathrm{\nu }}$

• ${\mathrm{\lambda }}_{\mathrm{0}}$ : longueur d’onde dans le vide (m)
• $\mathrm{T}$ : période (s)
• $\mathrm{\nu }$ : fréquence (Hz)
• $\mathrm{C}$ : célérité (m/s)

II- Caractéristiques d'une onde lumineuse

2-5/ Domaine des radiations lumineuses

Les valeurs des longueurs d’onde λ des radiations lumineuses nous permettent de les classer en différents domaines :

• Si $\mathrm{400}\mathrm{ }\mathrm{n}\mathrm{m}\mathrm{ }\mathrm{<}\mathrm{ }\mathrm{\lambda }\mathrm{ }\mathrm{<}\mathrm{ }\mathrm{800}\mathrm{ }\mathrm{n}\mathrm{m}$, la radiation appartient au domaine des radiations visibles (En effet l’oeil n’est sensible qu’à ce domaine de longueur d’onde, et nous permet de voir toutes les couleurs)
• Si $\mathrm{\lambda }\mathrm{ }\mathrm{<}\mathrm{ }\mathrm{400}\mathrm{ }\mathrm{n}\mathrm{m}$, la radiation appartient au domaine des ultraviolets.
• Si $\mathrm{\lambda }\mathrm{ }\mathrm{>}\mathrm{ }\mathrm{800}\mathrm{ }\mathrm{n}\mathrm{m}$, la radiation appartient au domaine des infrarouges.

III- Diffraction d’une onde lumineuse monochromatique

3-1/ Expérience

On utilise un LASER (Light Amplification by Simulated Emission of Radiation) émettant une lumière de longueur d’onde λ.

On dispose une fente fine verticale de largeur a dans le trajet lumineux et l’on observe sur un écran, situé à une distance D de la fente la diffraction. Avec L largeur la tâche centrale.

Influence de la largeur de la fente a

Plus la fente est fine et étroite, plus la lumière s’étale et plus la taille de la tâche centrale de la figure de diffraction est grande.

Influence de la longueur d’onde λ

Quand la longueur d’onde de la lumière incidente diminue, la largeur de la tache centrale diminue.

Influence de la distance D entre la fente et l’écran

Lorsque D augmente, la largeur L de la tache augmente aussi.

III- Diffraction d’une onde lumineuse monochromatique

3-2/ Écart angulaire

On appelle écart angulaire θ, l’angle, exprimé en radian, entre la droite passant par le milieu de la tache centrale et celle passant par le milieu de la première zone d’extinction.

$\overline{)\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{ }\mathrm{\theta }\mathrm{\approx }\mathrm{\theta }\left(rad\right)\mathrm{=}\frac{\mathrm{L}}{\mathrm{2}\mathrm{.}\mathrm{D}}}$

IV- Phénomène de dispersion de la lumière par un prisme

4-1/ Relations caractéristiques du prisme

Un prisme est formé d’un milieu transparent limité par deux faces planes. Il est caractérisé par son angle au sommet A et par son indice de réfraction n.

$$\begin{gathered} \overline{){\mathrm{n}}_{\mathrm{a}\mathrm{i}\mathrm{r}}\mathrm{.}\sin \left(i\right)\mathrm{=}\mathrm{n}\mathrm{.}\sin \left(r\right) \\ \mathrm{n}\mathrm{.}\sin (r\text{'})\mathrm{=}{\mathrm{n}}_{\mathrm{a}\mathrm{i}\mathrm{r}}\mathrm{.}\sin (i\text{'}) \\ \mathrm{A}\mathrm{=}\mathrm{r}\mathrm{+}\mathrm{r}\mathrm{\text{'}} \\ \mathrm{D}\mathrm{=}\mathrm{i}\mathrm{+}\mathrm{i}\mathrm{\text{'}}\mathrm{+}\mathrm{A}} \end{gathered}$$

IV- Phénomène de dispersion de la lumière par un prisme

4-2/ Dispersion de la lumière

La dispersion de la lumière blanche est sa décomposition en radiations monochromatiques (prisme) :

La dispersion d’une radiation monochromatique modifie seulement sa trajectoire :

IV- Phénomène de dispersion de la lumière par un prisme

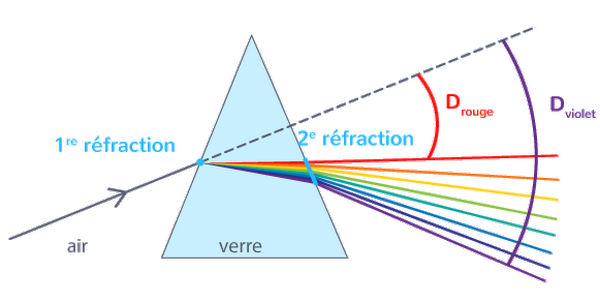
4-3/ Interprétation de la dispersion

Le prisme est constitué de deux surfaces de séparation. La première est la surface air-verre, appelée face d’entrée du prisme et la seconde est la surface verre-air, appelée face de sortie.

Le rayon lumineux incident subit une première réfraction sur la face d’entrée et une deuxième réfraction sur la face de sortie.

La lumière incidente est blanche elle est constituée d’une somme de radiations lumineuses. Toutes les radiations arrivent avec le même angle d’incidence i.

L'indice du prisme dépend de la fréquence (couleur de radiation) ou de la longueur d’onde dans le vide de la radiation

Selon la deuxième loi de la réfraction : sin(i)=n.sin(r) , le trajet d’une radiation dépend de l’indice du prisme .

Donc chaque radiation possède un angle de réfraction différent alors chaque radiation est déviée différemment.

V- Exercices

5-1/ Exercice 1

Pour déterminer la longueur d'onde d'une onde lumineuse on a éclairé une fente de largeur $\mathrm{a}\mathrm{=}\mathrm{5}\mathrm{.}{\mathrm{10}}^{\mathrm{-}\mathrm{5}}\mathrm{ }\mathrm{m}$ par un faisceau de lumière monochromatique.

On observe sur un écran qui se trouve à la distance $\mathrm{D}\mathrm{=}\mathrm{3}\mathrm{ }\mathrm{m}$ de la fente la formation de franges lumineuses

La mesure de la largeur de la frange centrale a donnée la valeur suivante : $\mathrm{L}\mathrm{=}\mathrm{7}\mathrm{,}\mathrm{6}\mathrm{.}{\mathrm{10}}^{\mathrm{-}\mathrm{2}}\mathrm{ }\mathrm{m}$

1. Comment s'appelle le phénomène étudié dans cette expérience ?
2. Donner l'expression de l'écart angulaire $\mathrm{\theta }$ en fonction de $\mathrm{D}$ et $\mathrm{L}$ (On prend : $\mathrm{t}\mathrm{a}\mathrm{n}\left(\theta \right)\mathrm{\approx }\mathrm{\theta }\left(rad\right)$
3. Calculerla la valeur de $\mathrm{\lambda }$.

V- Exercices

5-2/ Exercice 2

Partie 1 (Propagation d'une onde lumineuse)

Les fils de pêche de poissons se fabriquent actuellement en nylon pour qu'ils supportent la résistance du poisson chassé et ils sont de faible diamètre pour qu'ils ne soient pas être vus par les poissons.

Pour déterminer la valeur du diamètre a d'un fil, on l’a éclairé à l'aide d'un faisceau de lumière monchromatique de longueur d'onde $\mathrm{\lambda }$ dans l'air émis par une source laser.

On observe sur un écran qui se trouve à la distance $\mathrm{D}$ du fil la formation de franges, la largeur de la frange centrale est $\mathrm{L}$.

Données: $\mathrm{\lambda }\mathrm{=}\mathrm{623}\mathrm{,}\mathrm{8}\mathrm{ }\mathrm{n}\mathrm{m}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{D}\mathrm{=}\mathrm{3}\mathrm{ }\mathrm{m}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{L}\mathrm{=}\mathrm{7}\mathrm{,}\mathrm{5}\mathrm{ }\mathrm{c}\mathrm{m}$

1. Comment s'appelle le phénomène mis en évidence dans cette expérience ?

L'expression de l'écart angulaire $\mathrm{\theta }$ entre le milieu de la frange centrale et l'une de ses extrémités est $\mathrm{\theta }\mathrm{=}\frac{\mathrm{\lambda }}{\mathrm{a}}$.

2. Déterminer l'expression de $\mathrm{a}$ en fonction de $\mathrm{D}$ et $\mathrm{L}$ et $\mathrm{\lambda }$. Calculer la valeur de $\mathrm{a}$.

On remplace la source laser par une autre source laser de longueur d'onde $\mathrm{\lambda }\mathrm{\text{'}}$ et on obtient une frange centrale de de largeur $\mathrm{L}\mathrm{\text{'}}\mathrm{=}\mathrm{8}\mathrm{ }\mathrm{c}\mathrm{m}$.

3. Donner l'expression de $\mathrm{\lambda }\mathrm{\text{'}}$ en fonction de $\mathrm{\lambda }$, $\mathrm{L}$ et $\mathrm{L}\mathrm{\text{'}}$ .Calculer la valeur de $\mathrm{\lambda }\mathrm{\text{'}}$

Partie 2 (Détermination de la longueur d'onde d'une onde lumineuse dans le verre)

On envoie un faisceau lumineux monochromatique émis par une source laser sur la face d'un prisme en verre d'indice de réfraction $\mathrm{n}\mathrm{=}\mathrm{1}\mathrm{,}\mathrm{58}$.

4. Calculer la valeur de $\mathrm{V}$ vitesse de propagation du faisceau lumineux dans le prisme.

5. Déterminer la valeur de la longueur de l'onde lumineuse ${\mathrm{\lambda }}_{\mathrm{I}}$ durant sa propagation dans le prisme

Données:

• La longueur d'onde de l'onde lumineuse dans l'air est : ${\mathrm{\lambda }}_{\mathrm{0}}\mathrm{=}\mathrm{665}\mathrm{,}\mathrm{4}\mathrm{ }\mathrm{n}\mathrm{m}$
• La vitesse de propagation de la lumière dans le vide et dans l'air est $\mathrm{c}\mathrm{=}\mathrm{3}\mathrm{.}{\mathrm{10}}^{\mathrm{8}}\mathrm{ }\mathrm{m}\mathrm{/}\mathrm{s}$.

V- Exercices

5-3/ Exercice 3

On veut retrouver expérimentalement la longueur d'onde ${\mathrm{\lambda }}_{\mathrm{D}}$ de la radiation monochromatique du LASER d'un lecteur DVD. On utilise pour cela le montage de la figure ci-dessous, $\mathrm{a}$ étant le diamètre du fil et $\mathrm{\theta }$ l’écart angulaire.

1. Quel phénomène subit la lumière émise par le laser dans cette expérience ? Que peut-on en conclure par analogie avec les ondes mécaniques ?

2. On supposera $\mathrm{\theta }$ suffisamment petit pour considérer tan $\mathrm{t}\mathrm{a}\mathrm{n}\left(\theta \right)\mathrm{\approx }\mathrm{\theta }\left(rad\right)$. Établir la relation $\mathrm{L}\mathrm{=}\frac{\mathrm{2}\mathrm{.}{\mathrm{\lambda }}_{\mathrm{D}}\mathrm{.}\mathrm{D}}{\mathrm{a}}$ ($\mathrm{L}$ largeur de la tache centrale de diffraction et $\mathrm{D}$ distance entre le fil et l'écran).

On cherche maintenant à déterminer expérimentalement la longueur d'onde ${\mathrm{\lambda }}_{\mathrm{D}}$ de la lumière monochromatique émise par la source laser utilisée. Pour cela, on place devant le faisceau laser des fils calibrés verticaux.

La figure de diffraction obtenue est observée sur un écran blanc situé à une distance $\mathrm{D}\mathrm{=}\mathrm{2}\mathrm{,}\mathrm{50}\mathrm{ }\mathrm{m}$ des fils.

Pour chacun des fils, on mesure la largeur L de la tâche centrale de diffraction.

On trace la courbe L = f(1/a) représenté ci-dessous :

3. Donner l'équation de la courbe $\mathrm{L}\mathrm{ }\mathrm{=}\mathrm{ }\mathrm{f}\mathrm{(}\mathrm{1}\mathrm{/}\mathrm{a}\mathrm{)}$ et en déduire la longueur d'onde ${\mathrm{\lambda }}_{\mathrm{D}}$ de la lumière monochromatique constitutive du faisceau laser utilisé.

4. Calculer la fréquence ${\mathrm{\nu }}_{\mathrm{0}}$ de la lumière monochromatique émise par la source laser.

On remplace le fil par un cheveu d’épaisseur inconnu $\mathrm{e}$ et on mesure la longueur $\mathrm{L}\mathrm{\text{'}}$ de la tâche de diffraction obtenue.

La valeur de la tâche centrale mesurée sur l’écran est $\mathrm{L}\mathrm{’}\mathrm{=}\mathrm{20}\mathrm{ }\mathrm{m}\mathrm{m}$.

5. Calculer $\mathrm{e}$ l’épaisseur du cheveu.

6. Quelle aurait été approximativement la largeur de la tâche centrale si un laser vert avait été utilisé à la place du laser précédente ? Justifier.

Donnée : Célérité de la lumière dans le vide ou dans l’air: $\mathrm{c}\mathrm{ }\mathrm{=}\mathrm{3}\mathrm{,}\mathrm{00}\mathrm{.}{\mathrm{10}}^{\mathrm{8}}\mathrm{ }\mathrm{m}\mathrm{.}{\mathrm{s}}^{\mathrm{-}\mathrm{1}}$.

V- Exercices

5-4/ Exercice 4

L’objectif de cet exercice est d’étudier le phénomène de dispersion et celui de la diffraction.

Données : La vitesse de propagation d’une onde lumineuse dans l’air est approximativement égale à sa vitesse de propagation dans le vide : $\mathrm{c}\mathrm{=}\mathrm{3}\mathrm{,}\mathrm{00}\mathrm{.}{\mathrm{10}}^{\mathrm{8}}\mathrm{m}\mathrm{.}{\mathrm{s}}^{\mathrm{-}\mathrm{1}}$

Dispersion de la lumière

Un faisceau parallèle de lumière blanche arrive au point $\mathrm{I}$ de la surface d’un demi-disque en verre.

On observe sur l’écran (fig 1) les sept couleurs du spectre allant du rouge (R) au viole (V) :

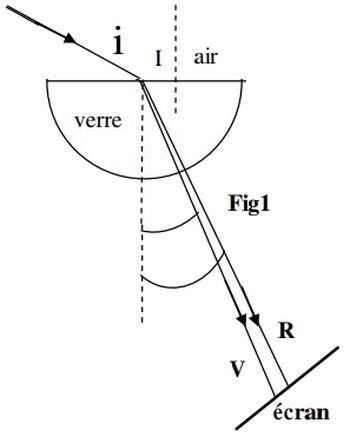
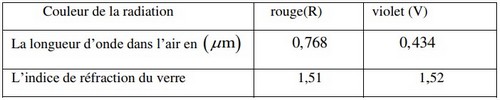
1. Exprimer la longueur d’onde ${\mathrm{\lambda }}_{\mathrm{R}}$ de la radiation rouge dans le verre en fonction de l’indice de réfraction ${\mathrm{n}}_{\mathrm{R}}$ du verre et de ${\mathrm{\lambda }}_{\mathrm{0}\mathrm{R}}$ (longueur d’onde dans l’air de ce rayonnement).

L’indice de réfraction $\mathrm{n}$ d’un milieu transparent pour une radiation monochromatique de longueur d’onde ${\mathrm{\lambda }}_{\mathrm{0}}$ dans l’air est modélisé par la relation $\overline{)\mathrm{n}\mathrm{=}\mathrm{A}\mathrm{+}\frac{\mathrm{B}}{{{\mathrm{\lambda }}_{\mathrm{0}}}^{\mathrm{2}}}}$, dont A et B sont des constantes qui dépendent du milieu.

2. Calculer la valeur de A et celle de B pour le verre utilisé

Diffraction de la lumière

On réalise l’expérience de la diffraction d’une lumière monochromatique de longueur d’onde $\mathrm{\lambda }$ dans l’air émise par un dispositif laser, en utilisant une fente de largeur $\mathrm{a}$ comme l’indique la
figure 2 :

On mesure la largeur $\mathrm{d}$ de la tache centrale pour différentes valeurs de la largeur $\mathrm{a}$ de la fente et on représente graphiquement $\mathrm{d}\mathrm{=}\mathrm{f}\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$a$}\right.\right)$ , on obtient alors la courbe indiquée dans la figure 3 :

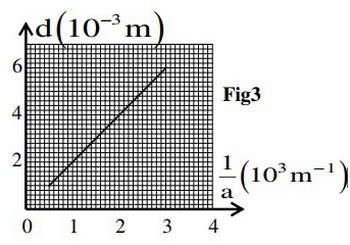
3. Trouver l’expression de $\mathrm{d}$ en fonction de $\mathrm{\lambda }$ et $\mathrm{a}$ et $\mathrm{D}$, sachant que $\mathrm{\theta }\mathrm{=}\frac{\mathrm{\lambda }}{\mathrm{a}}$ ($\mathrm{\theta }$ petit exprimé en rad)

4. À l’aide de la figure 3, déterminer la valeur de $\mathrm{\lambda }$.