Séance 12 - Bissectrices et hauteurs d’un triangle

Sommaire

I- Bissectrice

1-1/ Définition

1-2/ Propriété

1-3/ Bissectrice d’un triangle

II- Hauteurs d’un triangle

2-1/ Définition

2-2/ Propriété

2-3/ Cas particuliers

III- Exercices

3-1/ Exercice 1

3-2/ Exercice 2

3-3/ Exercice 3

3-4/ Exercice 4

3-5/ Exercice 5

3-6/ Exercice 6

I- Bissectrice

1-1/ Définition

La bissectrice d'un angle est la demi-droite qui partage l'angle en deux angles adjacents de même mesure.

Exemple

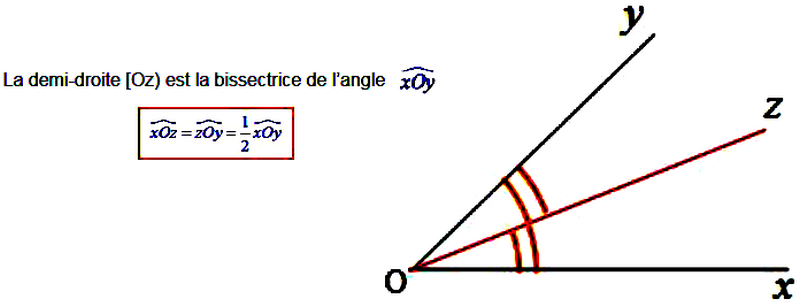
1-2/ Propriété

Si un point appartient à la bissectrice d’un angle, alors il est équidistant des côtés de cet angle.

Exemple

Le point M appartient à la bissectrice de l'angle HAH', donc MH = MH'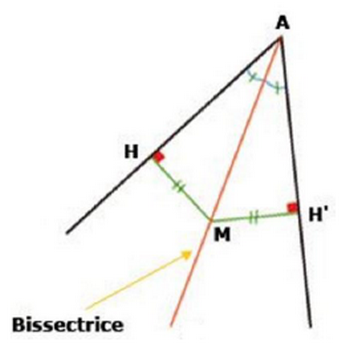

I- Bissectrice

1-3/ Bissectrice d’un triangle

Définition

Une bissectrice d’un triangle est une bissectrice de l’un de ses angles.

Propriété

Les trois bissectrices d'un triangle sont concourantes en un point appelé centre du cercle inscrit au triangle.

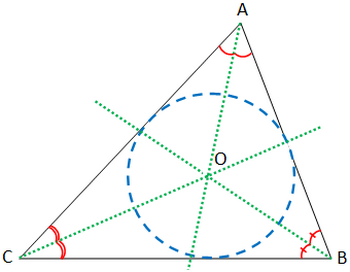
Remarque

Pour construire le centre du cercle inscrit, il suffit de tracer deux bissectrices de ce triangle.

II- Hauteurs d’un triangle

2-1/ Définition

La hauteur d’un triangle est la droite qui passe par l’un des sommets de ce triangle et perpendiculaire au support de côté opposé à ce sommet.

Exemple

(AH) est la hauteur issue du sommet A

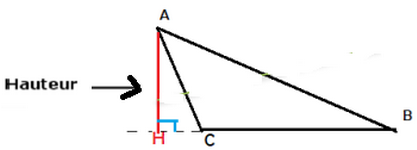II- Hauteurs d’un triangle

2-2/ Propriété

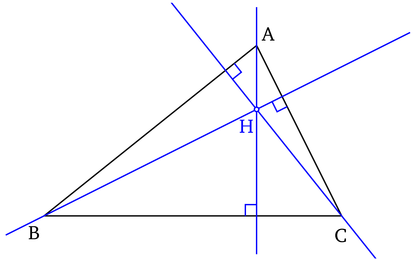
Les hauteurs d’un triangle sont concourantes en un seule point appelé orthocentre de ce triangle.

Exemple

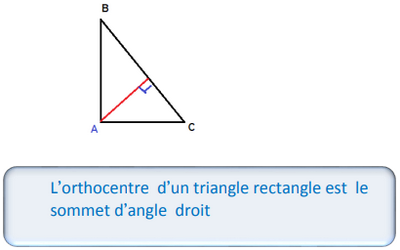
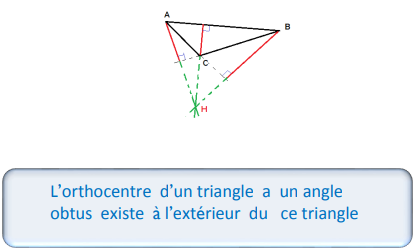
2-3/ Cas particuliers

III- Exercices

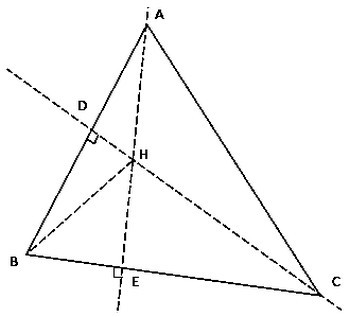
3-1/ Exercice 1

A- Dans le triangle ABC : Quelle est la hauteur issue de A ?      Quelle est la hauteur issue de C ? Quel est l’orthocentre du triangle Quelle est la hauteur relative à [AC] ?  B- Dans le triangle BCH : Quelle est la hauteur relative à [BC] ?     Quelle est la hauteur issue de B ?     Quel est l’orthocentre du triangle ? Quelle est la hauteur relative à [BH] ?  C- Dans le triangle ABH : Quelle est la hauteur relative à [AB] ?     Quelle est la hauteur relative à [AH] ?        Quel est l’orthocentre du triangle ? Quelle est la hauteur relative à [BH] ?

III- Exercices

3-2/ Exercice 2

1) Dans la figure ci-contre : Tracer F le point d'intersection des deux droites (CD) et (BE) 2) Montrer que (AF) ⊥ (BC)

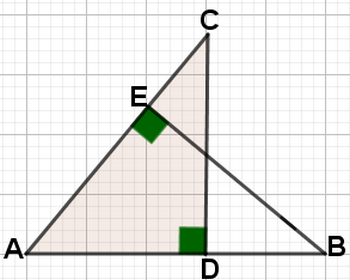III- Exercices

3-3/ Exercice 3

Dans la figure suivante, I est le centre du cercle inscrit dans le triangle ABC On donne : $\widehat{\mathrm{E}\mathrm{B}\mathrm{C}}\mathrm{=}\mathrm{32}\mathrm{°}$ et $\widehat{\mathrm{D}\mathrm{C}\mathrm{B}}\mathrm{=}\mathrm{25}\mathrm{°}$ 1) Calculer $\widehat{\mathrm{A}\mathrm{B}\mathrm{C}}$ et $\widehat{\mathrm{A}\mathrm{C}\mathrm{B}}$ . Justifier les réponses. 2)Déterminer les mesures des angles $\widehat{\mathrm{B}\mathrm{A}\mathrm{C}}$ puis $\widehat{\mathrm{B}\mathrm{A}\mathrm{I}}$ . Justifier.

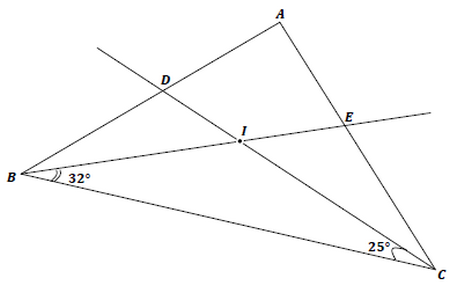III- Exercices

3-4/ Exercice 4

$ABC$ est un triangle isocèle de sommet A tel que : $\widehat{\mathrm{ABC}}=50°$ et $BC=4cm$

$\left(AH\right)$ est la hauteur issue du point $A$

1) Dessiner une figure convenable

2)

a) Calculer en justifiant : $\widehat{\mathrm{HAC}}$ et $\widehat{\mathrm{HAB}}$

b) En déduire que la demi-droite $\mathrm{\left[}\mathrm{A}\mathrm{H}\mathrm{\right)}$ est la bissectrice de l’angle $\widehat{\mathrm{BAC}}$

3)

a) Tracer la bissectrice de l’angle $\widehat{\mathrm{ACB}}$ , tel qu’elle coupe le segment $\left[AH\right]$ en $M$

b) Calculer en justifiant $\widehat{\mathrm{CMH}}$

c) Prouver que $\left[BM\right)$ est la bissectrice de $\widehat{\mathrm{ABC}}$

III- Exercices

3-5/ Exercice 5

$MAD$ est un triangle tels que $AP=6cm$, $\widehat{MAP}=80°$ et $\widehat{MPA}=40°$.

La bissectrice de $\widehat{MAP}$ coupe $\left[MP\right]$ en $I$.

1. Faire une figure.

2. Comparer $Al$ et $IP$.

La bissectrice de l'angle $\widehat{AMP}$ coupe $\left(Al\right)$ en $O$.

3. Déterminer la mesure de $\widehat{OPA}$, en justifiant la réponse.

Soit $N$ le milieu de $\left[AP\right]$.

4. Montrer que $\left(NI\right)\perp \left(AP\right)$.

III- Exercices

3-6/ Exercice 6

1. Peut-on construire un triangle $ABC$ tels que $AB=2cm$, $AC=4,5cm$ et $BC=3cm$ ? justifier.

2. Construire le triangle $ABC$, puis placer le point $H$, intersection de la perpendiculaire à $\left(BC\right)$ passant par $A$ et la perpendiculaire à $\left(AB\right)$ passant par $C$.

3. Que représente le point $H$ pour le triangle $ABC$ ? justifier.

4. Montrer que $\left(BH\right)\perp \left(AC\right)$.

5. Quel est l'orthocentre du triangle $HBC$ ? justifier.

6. Quel est l'orthocentre du triangle $ABH$ ? justifier.