Séance 10 - Puissances

Sommaire

I- Puissance d’un nombre relatif

1-1/ Définition

1-2/ Signe d’une puissance

1-3/ Puissance de 10

II- Propriétés des puissances

2-1/ Produit de deux puissances de même base

2-2/ Produit de deux puissances de même exposant

2-3/ Puissance d’une puissance

2-4/ Quotient  de deux puissances de même base

2-5/ Quotient de deux puissances de même exposant

III- Exercices

3-1/ Exercice 1

3-2/ Exercice 2

3-3/ Exercice 3

3-4/ Exercice 4

3-5/ Exercice 5

3-6/ Exercice 6

I- Puissance d’un nombre relatif

1-1/ Définition

Soient un nombre relatif et un nombre entier naturel non nul:

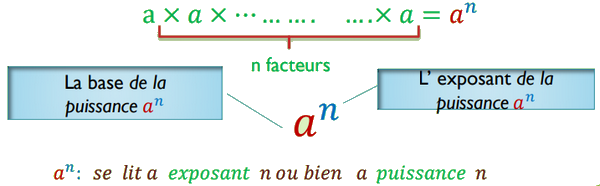
Exemple

Cas particuliers

• ${\mathrm{a}}^{\mathrm{1}}\mathrm{=}\mathrm{a}$
• ${\mathrm{a}}^{\mathrm{0}}\mathrm{=}\mathrm{1}$ si $\mathrm{a}\mathrm{\ne }\mathrm{0}$
• ${\mathrm{a}}^{\mathrm{2}}$ se lit « a  au carré »
• ${\mathrm{a}}^{\mathrm{3}}$ se lit « a  au cube »

I- Puissance d’un nombre relatif

1-2/ Signe d’une puissance

a est un nombre relatif, et n un nombre entier non nul.

• Si l’exposant n est pair alors la puissance ${\mathrm{a}}^{\mathrm{n}}$ est positive
• Si l’exposant n est impair alors la puissance ${\mathrm{a}}^{\mathrm{n}}$ prend le signe de la base a.

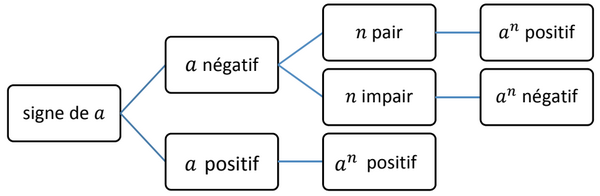
Exemple

I- Puissance d’un nombre relatif

1-3/ Puissance de 10

Soit un nombre entier naturel non nul.

Exemple

II- Propriétés des puissances

2-1/ Produit de deux puissances de même base

Propriété

Soient a un nombre relatif et m et n deux nombres entiers naturels non nuls.

$\overline{){\mathrm{a}}^{\mathrm{m}}\mathrm{\times }{\mathrm{a}}^{\mathrm{n}}\mathrm{=}{\mathrm{a}}^{(m+n)}}$

Exemple

2-2/ Produit de deux puissances de même exposant

Propriété

Soient a et b deux nombres relatifs et n un nombre entier naturel non nul

$\overline{){\mathrm{a}}^{\mathrm{n}}\mathrm{\times }{\mathrm{b}}^{\mathrm{n}}\mathrm{=}{(a\times b)}^{\mathrm{n}}}$

Exemple

II- Propriétés des puissances

2-3/ Puissance d’une puissance

Propriété

Soient a un nombre relatif et m et n deux nombres entiers naturels non nuls.

$\overline{){\left(a^m\right)}^{\mathrm{n}}\mathrm{=}{\left(a\right)}^{\mathrm{m}\mathrm{\times }\mathrm{n}}}$

Exemple

2-4/ Quotient  de deux puissances de même base

Propriété

Soient a un nombre relatif et m et n deux nombres entiers naturels non nuls tel que : $\mathrm{n}\mathrm{>}\mathrm{m}$

$\overline{)\frac{{\mathrm{a}}^{\mathrm{n}}}{{\mathrm{a}}^{\mathrm{m}}}\mathrm{=}{\mathrm{a}}^{\mathrm{n}\mathrm{-}\mathrm{m}}\mathrm{ }\mathrm{ }(n>m)}$

Exemple

II- Propriétés des puissances

2-5/ Quotient de deux puissances de même exposant

Propriété

Soient a et b deux nombres relatifs et n un nombre entier naturel non nul

$\overline{)\frac{{\mathrm{a}}^{\mathrm{n}}}{{\mathrm{b}}^{\mathrm{n}}}\mathrm{=}{\left(\frac{a}{b}\right)}^{\mathrm{n}}}$

Exemple

III- Exercices

3-1/ Exercice 1

Calculer :

$$\begin{gathered} \overline{){\mathrm{9}}^{\mathrm{2}}\mathrm{=}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{ } \\ {(-5)}^{\mathrm{3}}\mathrm{=}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{ } \\ {(-2)}^{\mathrm{6}}\mathrm{=}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{ } \\ {(-1)}^{\mathrm{320}}\mathrm{=}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{ } \\ {\mathrm{0}}^{\mathrm{1937}}\mathrm{=}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{ } \\ {(-4)}^{\mathrm{4}}\mathrm{=}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{ } \\ {\mathrm{513}}^{\mathrm{0}}\mathrm{=}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{ } \\ {\mathrm{1}}^{\mathrm{715}}\mathrm{=}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{ } \\ {\mathrm{10}}^{\mathrm{7}}\mathrm{=}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{ } \\ {(1,2)}^{\mathrm{3}}\mathrm{=}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{\_}\mathrm{ }} \end{gathered}$$

III- Exercices

3-2/ Exercice 2

Calculer :

III- Exercices

3-3/ Exercice 3

Déterminer le signe en justifiant votre réponse :

$\overline{){\mathrm{(}\mathrm{-}\mathrm{19}\mathrm{)}}^{\mathrm{3}}\mathrm{ }\mathrm{;}\mathrm{ }{\mathrm{3}}^{\mathrm{19}}\mathrm{ }\mathrm{;}\mathrm{ }{\mathrm{(}\mathrm{-}\mathrm{7}\mathrm{,}\mathrm{8}\mathrm{)}}^{\mathrm{13}}\mathrm{ }\mathrm{;}\mathrm{ }{\mathrm{(}\mathrm{-}\mathrm{3}\mathrm{)}}^{\mathrm{16}}\mathrm{ }\mathrm{;}\mathrm{ }{\mathrm{24}}^{\mathrm{2}}\mathrm{ }\mathrm{;}\mathrm{ }{\mathrm{(}\mathrm{-}\mathrm{15}\mathrm{)}}^{\mathrm{11}}\mathrm{ }\mathrm{;}\mathrm{ }{\mathrm{(}\mathrm{-}\mathrm{8}\mathrm{)}}^{\mathrm{6}}\mathrm{ }\mathrm{;}\mathrm{ }{\mathrm{13}}^{\mathrm{5}}}$

III- Exercices

3-4/ Exercice 4

Écrire chacune des expressions suivantes sous la forme d’une puissance :

III- Exercices

3-5/ Exercice 5

On donne :

 $$\begin{gathered} Z=0,39\times {10}^{47}+610\times {10}^{44} \\ T=1075\times {10}^{53}-0,75\times {10}^{55} \end{gathered}$$

1. Montrer que $Z$ et $T$ sont deux puissances de $10$.

III- Exercices

3-6/ Exercice 6

Un professeur de mathématiques demande à ses élèves de calculer les expressions suivantes :

$$\begin{gathered} a={\left(-2\right)}^5+32 \\ b=\frac{9-6\times 3}{9}-\left(-1\right) \\ c=\left(-1,25\right)\times \left(-8\right)-2^{15}\times {10}^{-14}\times 5^{15} \end{gathered}$$

Après un moment de recherche, Samir affirme que $a=b=c$.

Nawal intervient et dit : " Pas exactement, j'ai trouvé $a=b=0$ alors que $c=-17$ ".

1. À votre avis, qui a raison ? Justifier par des calculs détaillés.

2. Trouver l'erreur de celui qui a tort.