Séance 7 - Nombres relatifs (Présentation et comparaison)

Sommaire

I- Définition

II- Se repérer sur un axe gradué dans le plan

III- La distance à zéro

IV- Deux nombres relatifs opposés

V- Comparaison des  nombres relatifs

5-1/ Règle 1

5-2/ Règle 2

5-3/ Règle 3

VI- Exercices

6-1/ Exercice 1

6-2/ Exercice 2

6-3/ Exercice 3

6-4/ Exercice 4

6-5/ Exercice 5

6-6/ Exercice 6

I- Définition

L’ensemble des nombres relatifs est composé de deux types de nombres:

• Les nombres positifs

On peut écrire ces nombres avec un signe "+",mais ce n’est pas obligatoire.

Exemples: +7 , +1,04 , 15,6 et 23 sont des nombres positifs.

• Les nombres négatifs

On écrit toujours ces nombres avec un signe "−".

Exemples: −4 , −5,2 et −56 sont des nombres négatifs.

Il existe un seul nombre qui est  à la fois positif et négatif : c’est zéro (0)

II- Se repérer sur un axe gradué dans le plan

On appelle axe gradué une droite sur laquelle on a choisi un sens, un point nommé origine et une unité que l’on reporte régulièrement à partir de l’origine.

Sur cet axe gradué :

• À chaque point de la droite est associé un unique nombre relatif, qui est appelé abscisse du point.
• À chaque nombre relatif est associé un unique point de la droite

Par exemple, l’abscisse du point A est +4, le point d’abscisse −6 est B.

III- La distance à zéro

La distance à zéro d’un nombre relatif est le nombre d’unités qui séparent ce point de l’origine.

Par exemple :

• la distance à zéro du nombre +4 est 4 (car le segment [OA] mesure 4 unités de long),
• la distance à zéro du nombre −6 est 6 (car le segment [OB] mesure 6 unités de long).

IV- Deux nombres relatifs opposés

Deux nombres relatifs qui ont la même distance à zéro, mais des signes différents, sont appelés nombres opposés.

Par exemple :

• Les nombres +6 et −6 ont la même distance à zéro (6), mais pas le même signe : ce sont deux nombres opposés.
• L’opposé de 7 est −7
• l’opposé de −3 est 3.

V- Comparaison des  nombres relatifs

5-1/ Règle 1

De deux nombres relatifs positifs, le plus grand est celui ayant la plus grande distance à zéro.

Exemple

On a +4 < +6 car +6 a la plus grande distance à zéro.

5-2/ Règle 2

De deux nombres relatifs de signes contraires, le plus grand est le nombre positif.

Exemple

On a +4 > −1 car +4 est positif (et −1 est négatif ).

5-3/ Règle 3

De deux nombres relatifs négatifs, le plus grand est celui ayant la plus petite distance à zéro.

Exemple

On a −6 < −1 car −1 a la plus petite distance à zéro.

VI- Exercices

6-1/ Exercice 1

1) Complétez les phrases suivantes:

• (+3.2), (+7000), 0, (+14.81) sont des nombres __________________ .
• (-3.2), (-200,01), 0, (-14,81) sont des nombres __________________ .
• (-3.7) est l’opposé de (+3,7), donc: (+701) est __________________ .de (-701) et (+14,726) est l’opposé de ( __________________ .)

2) Complétez avec le mot qui convient :

positif – négatif - plus - relatif - opposé - moins

• −3 ; + 5 ; – 9,3 ; 100,07 sont des nombres __________________ .
• Le nombre + 5 est un nombre __________________ . Il peut aussi s'écrire sans le signe __________________ .
• Le nombre – 5 est un nombre __________________ . On ne peut pas supprimer le signe  __________________ .
• Le nombre 0 est à la fois __________________ et __________________ .
• – 3 est __________________ de + 3.

VI- Exercices

6-2/ Exercice 2

1) Comparez les nombres relatifs suivants:

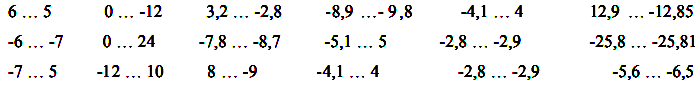
2) Rangez dans l’ordre croissant

$\overline{)\mathrm{ }\mathrm{-}\mathrm{2}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{3}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{0}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{-}\mathrm{2}\mathrm{,}\mathrm{5}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{2}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{3}\mathrm{,}\mathrm{5}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{-}\mathrm{3}\mathrm{,}\mathrm{51}\mathrm{ }}$

$\overline{)\mathrm{ }\mathrm{-}\mathrm{2}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{0}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{-}\mathrm{2}\mathrm{,}\mathrm{45}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{-}\mathrm{5}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{1}\mathrm{,}\mathrm{23}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{-}\mathrm{6}\mathrm{,}\mathrm{4}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{13}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{14}\mathrm{ }}$

3) Rangez dans l’ordre décroissant

$\overline{)\mathrm{ }\mathrm{4}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{-}\mathrm{4}\mathrm{,}\mathrm{5}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{2}\mathrm{,}\mathrm{75}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{-}\mathrm{2}\mathrm{,}\mathrm{1}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{-}\mathrm{2}\mathrm{,}\mathrm{01}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{-}\mathrm{4}\mathrm{,}\mathrm{51}\mathrm{ }}$

$\overline{)\mathrm{ }\mathrm{7}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{-}\mathrm{2}\mathrm{,}\mathrm{6}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{1}\mathrm{,}\mathrm{12}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{-}\mathrm{3}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{15}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{0}\mathrm{ }\mathrm{;}\mathrm{ }\mathrm{-}\mathrm{4}\mathrm{,}\mathrm{2}\mathrm{ }}$

VI- Exercices

6-3/ Exercice 3

1) Donnez les abscisses des points A, E, F et I.

2) Placez les points L(– 3) ; R(– 6) et S(6).

3) Placez le point T symétrique de I par rapport à l’origine. Quelle est l’abscisse de T ?

4) Quel mot peux-tu lire ?

VI- Exercices

6-4/ Exercice 4

1) Donnez tous les nombres entiers relatifs qui sont comprise entre -5,3 et 4,9.

2) Donnez tous les nombres entiers relatifs dont la distance à zéro est comprise entre 12,8 et 20,1.

3) Donnez les opposés des nombres suivants :

VI- Exercices

6-5/ Exercice 5

1. Tracer une droite graduée d'origine O, et placer les points A, B, C et D d'abscisses respectives : 4 ; 3 ; -3,25 ; 2.

2. Colorier en rouge les points d'abscisses compris entre -3,25 et 0.

3. Placer les points A', B', C' et D' d'abscisses les opposés des abscisses de A, B, C et D.

VI- Exercices

6-6/ Exercice 6

(D) est une droite graduée d'origine O.

Soit A un point de (D) d'abscisse -3,5.

1. Placer A sur (D).

2. Placer le point E tel que E appartient à la demi-droite [OA) et OE=4,5.

3. Placer le point F tel que F appartient à la demi-droite [AO) et OF=4,5.

4. Quelle est l'abscisse du point E ? du point F ?

5. Que peut-on dire des abscisses de E et F ?