Séance 5 - Inégalité triangulaire et médiatrice d’un segment

Sommaire

I- Inégalité triangulaire

1-1/ Positions d’un point et un segment

1-2/ Propriété

II- Médiatrice d’un segment

2-1/ Définition

2-2/ Propriété directe

2-3/ Propriété réciproque

III- Médiatrices d’un triangle

3-1/ Définition

3-2/ Propriété

3-3/ Cas particuliers

IV- Exercices

4-1/ Exercice 1

4-2/ Exercice 2

4-3/ Exercice 3

4-4/ Exercice 4

4-5/ Exercice 5

4-6/ Exercice 6

I- Inégalité triangulaire

1-1/ Positions d’un point et un segment

a) Si un point n’appartient pas à un segment :

b) Si un point appartient à un segment :

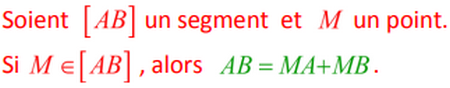
1-2/ Propriété

Dans un triangle, la longueur de chaque côté est strictement inférieure à la somme des longueurs des deux autres.

II- Médiatrice d’un segment

2-1/ Définition

La médiatrice d’un segment est la droite perpendiculaire à ce segment en son milieu.

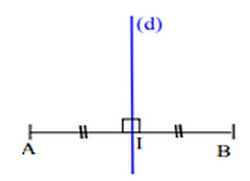
2-2/ Propriété directe

Si un point appartient à la médiatrice d’un segment, alors il est équidistant à ses extrémités.

2-3/ Propriété réciproque

Si un point est équidistant des extrémités d’un segment, alors il appartient à la médiatrice de ce segment.

III- Médiatrices d’un triangle

3-1/ Définition

La médiatrice d’un triangle est la médiatrice de l’un de ses côtés.  

Exemple

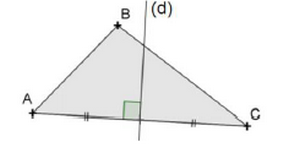
La droite (d) est une médiatrice du triangle ABC

3-2/ Propriété

Les médiatrices des côtés d'un triangle sont concourantes en un point qui est le centre du cercle circonscrit à ce triangle

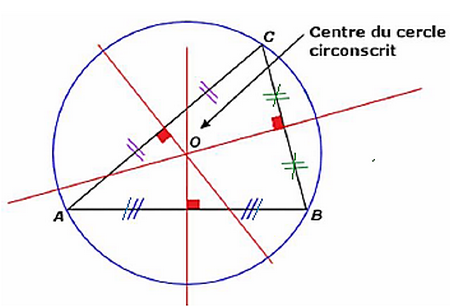
3-3/ Cas particuliers

IV- Exercices

4-1/ Exercice 1

1) Compléter:

• Pour un triangle ABC A,B et C sont ____________________ .
• [AB], [BC] et [AC] sont ____________________ .

2) Sans faire de dessin, peut-on construire ces trois triangles ? Explique pourquoi.

• ABC avec AB=7cm , AC=3cm et BC=5cm.
• DEF avec DE=2cm , EF=6cm et DF=3cm.
• OIJ avec OJ=4cm , IJ=6cm et OI=10cm

IV- Exercices

4-2/ Exercice 2

Dans quels cas la droite (d) est-elle la médiatrice de [AB] ? Justifier la réponse.

IV- Exercices

4-3/ Exercice 3

1) Construire trois points A, B et C alignés dans cet ordre tel que AB = 5 cm et BC = 5,8 cm.

2) Construire la médiatrice (d) de [AB] et (d') la médiatrice de [BC].

3) Démontrer que (d) et (d') sont parallèles.

IV- Exercices

4-4/ Exercice 4

Tracer un cercle (C) de centre O et de Rayon 2 cm

Placer deux point A et B sur le cercle (C) tel que AB = 3 cm

Tracer la corde [AB]

Placer le point M milieu de [AB]

Montrer que (OM) et La médiatrice de segment [AB]

IV- Exercices

4-5/ Exercice 5

Trois chiens sont dans des enclos.

La figure suivante permet de situer les piquets auquel chaque chien est attaché. Une longueur d'un centimètre sur le dessin correspond à une longueur d'un mètre en réalité :

Chaque laisse qui relie un chien au piquet a une longueur de $3m$.

1. Mettre en couleur la zone que les trois chiens peuvent atteindre.

On doit placer une gamelle commune aux trois chiens.

2. Situer le point $M$ représentant la position de la gamelle qui soit équidistante aux piquets des trois chiens. Expliquer.

IV- Exercices

4-6/ Exercice 6

$M$ est un point situé à l'intérieur de l'angle $\overbrace{BAC}$ :

1. Placer le point $P$ pour que $\left(AB\right)$ soit la médiatrice de $\left[MP\right]$.

2. Placer le point $Q$ pour que $\left(AC\right)$ soit la médiatrice de $\left[MQ\right]$.

3. Déterminer en justifiant la réponse, le centre du cercle circonscrit au triangle $MPQ$.