Séance 4 - Notions de base de la géométrie dans le plan

Sommaire

I- Les figures géométriques usuelles

1-1/ Les points

1-2/ Les droites

1-3/ Les demi-droites

1-4/ Les segments

1-5/ Appartenance, points alignés

II- Positions de deux droites

2-1/ Droites sécantes

2-2/ Droites perpendiculaires

2-3/ Droites parallèles

III- Propriétés de trois droites

3-1/ Propriété 1

3-2/ Propriété 2

3-3/ Propriété 3

3-4/ Propriété 4

IV- Exercices

4-1/ Exercice 1

4-2/ Exercice 2

4-3/ Exercice 3

4-4/ Exercice 4

4-5/ Exercice 5

4-6/ Exercice 6

4-7/ Exercice 7

I- Les figures géométriques usuelles

1-1/ Les points

Dans un plan, il y a une infinité de points.

On les représente par une croix:

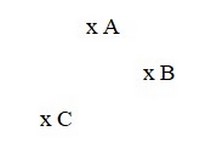
1-2/ Les droites

Une droite est formée par une infinité de points alignés.

Une droite n’a pas de longueur, elle est illimitée, on ne peut pas la mesurer.

On note :

Régle 1

par un point passe une infinité de droites

Exemple

Régle 2

par deux points passe une seule droite

Exemple

I- Les figures géométriques usuelles

1-3/ Les demi-droites

Tout point A sur une droite définit deux demi-droites.

Les deux demi-droites ont pour origine le point A,  on les note : [Ax)  et [Ay)

Une demi-droite n’a pas de longueur.

La demi-droite d’origine A contenant le point B se note : [AB)

I- Les figures géométriques usuelles

1-4/ Les segments

L’ensemble des points de la droite situés entre T et R forme un segment, qu'on note : [TR]

Les points T et R sont les extrémités du segment.

La longueur du segment [TR] est notée : TR.

Le milieu du segment est le point qui le partage en deux segments de même longueur.

I est le milieu du segment [AB]

Alors : AI = IB.

I- Les figures géométriques usuelles

1-5/ Appartenance, points alignés

Appartenance

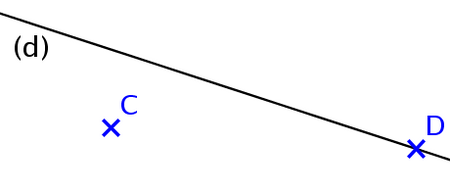
Le point D appartient à la droite (d).

On note : $\mathrm{D}\mathrm{\in }\mathrm{\left(}\mathrm{d}\mathrm{\right)}$

Le point C n’appartient pas à la droite (d).

On note : $\mathrm{C}\mathrm{\notin }\left(d\right)$

Points alignés

Les points alignés sont des points qui appartiennent à une  même droite:

Les points A, B et C sont alignés

II- Positions de deux droites

2-1/ Droites sécantes

Deux droites sécantes sont deux droites qui n’ont qu’un  seule point commun.

2-2/ Droites perpendiculaires

Deux droites perpendiculaires sont deux droites sécantes qui forment quatre angles droits.

2-3/ Droites parallèles

Deux droites parallèles sont deux droites non sécantes.

III- Propriétés de trois droites

3-1/ Propriété 1

Lorsque deux droites sont parallèles, toute perpendiculaire à l’une est perpendiculaire à l’autre.

3-2/ Propriété 2

Lorsque deux droites sont parallèles, toute droite parallèle à l’une est parallèle à l’autre.

3-3/ Propriété 3

Lorsque deux droites sont perpendiculaires, toute droite perpendiculaire à l’une est parallèle à l’autre.

3-4/ Propriété 4

Lorsque deux droites sont perpendiculaires, toute droite parallèle à l’une est perpendiculaire à l’autre.

IV- Exercices

4-1/ Exercice 1

Remplir les vides:

• [AB] est _____________ ,(AB) est _____________ , AB est _____________ .
• Le point A appartient à la droite (d). On note _____________ .
• Le point M n’appartient pas à la droite (d). On note _____________ .
• Les points A, B et C appartiennent à la droite (d).  On dit que A, B et C sont _____________ .

IV- Exercices

4-2/ Exercice 2

Compléter les pointillés du tableau par le signe $\mathrm{"}\mathrm{\in }\mathrm{"}$ ou le signe $\mathrm{"}\mathrm{\notin }\mathrm{"}$:

IV- Exercices

4-3/ Exercice 3

1- Tracer la droite (d1) passant par le point M et perpendiculaire à la droite (d).

2- Tracer la droite (d2) passant par le point C et perpendiculaire à la droite (d).

3- Tracer la droite (d3) passant par le point N et perpendiculaire à la droite (d).

4- Que peut-on dire de droites (d1), (d2) et (d3) ?

5- Tracer la droite (d5) passant par M et perpendiculaire à (d1). Que peut-on dire de droites (d) et (d5) ?

IV- Exercices

4-4/ Exercice 4

1- Observer la figure ci-dessous et compléter les phrases à l'aide du vocabulaire adapté : Les droites (MQ) et (RN) sont __________________ Les points S, R et P sont __________________ Les droites (MN) et (QP) sont __________________ Les droites (SL) et ( MV) sont __________________ Les droites (TU) et (SL) sont __________________ Le point S est __________________ des droites (IL ) et (RP) 2- Compléter à l'aide des symboles $\mathrm{\parallel }$ ou $\mathrm{\perp }$ lorsque cela est possible: (LS) ____ (UR) – (MN) ____ (OP) (SR) ____ (OP) – (SR) ____ (QP)

IV- Exercices

4-5/ Exercice 5

1) Compléter le raisonnement suivant: Les droites (BE) et (AD) sont _________________ de même que les droites (DG) et _________. Or si deux droites sont _________ à une droite, alors elles sont _________. Donc les droites (BE) et _________ sont _________ . 2) Compléter le raisonnement suivant: Les droites _________ et (DF) sont parallèles et les droites _________ et (AG) sont perpendiculaires. Or si deux droites sont _________ et si une droite est _________ à l'une,  alors elle est _________ à l'autre. Donc les droites _________ et (AG) sont _________ .

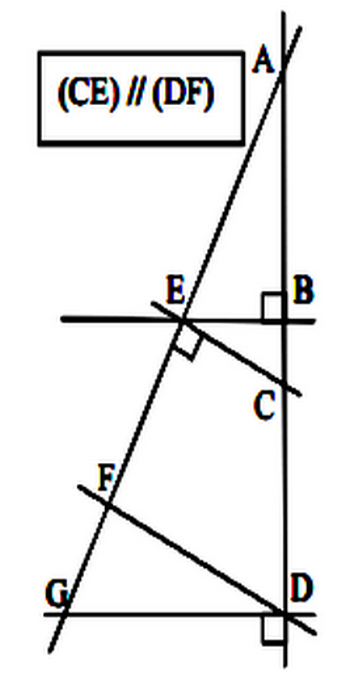IV- Exercices

4-6/ Exercice 6

I est le milieu d’un segment [MN] et MI = 4,2 cm.

1) Calculer la longueur MN.

2) Tracer le segment [MN], puis construis le point I

IV- Exercices

4-7/ Exercice 7

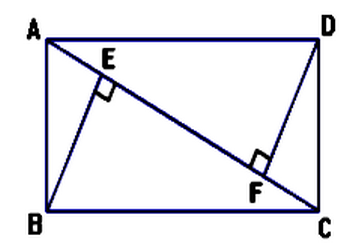ABCD est un rectangle La droite (BE) est perpendiculaire à (AC) La droite (DF) est perpendiculaire à (AC) Démontrer que (BE) et (DF) sont parallèles