Séance 1 - Opérations sur les nombres entiers et décimaux

Sommaire

I- Vocabulaire

1-1/ Addition et somme

1-2/ Soustraction et différence

1-3/ Multiplication et produit

1-4/ Division et quotient

II- Expressions sans parenthèses: priorités opératoires

2-1/ Propriété 1

2-2/ Propriété 2

III- Expressions avec parenthèses

3-1/  Propriété

IV- Distributivité

4-1/  Propriété

V- Exercices

5-1/ Exercice 1

5-2/ Exercice 2

5-3/ Exercice 3

5-4/ Exercice 4

5-5/ Exercice 5

5-6/ Exercice 6

I- Vocabulaire

1-1/ Addition et somme

L’addition est une opération.

La somme est le résultat d’une addition.

I- Vocabulaire

1-2/ Soustraction et différence

La soustraction est une opération.

La différence est le résultat d’une soustraction.

I- Vocabulaire

1-3/ Multiplication et produit

La multiplication est une opération.

Le produit est le résultat d’une multiplication.

I- Vocabulaire

1-4/ Division et quotient

La division est une opération.

Le quotient est le résultat d’une division.

II- Expressions sans parenthèses: priorités opératoires

2-1/ Propriété 1

Dans une expression sans parenthèses avec uniquement des additions et des soustractions, on effectue les calculs de gauche à droite.

Dans une expression sans parenthèses avec uniquement des multiplications et des divisions, on effectue les calculs de gauche à droite.

Exemple

II- Expressions sans parenthèses: priorités opératoires

2-2/ Propriété 2

Dans une expression sans parenthèses on effectue les multiplications et les divisions avant les additions et les soustractions.

On dit que la multiplication et la division sont Prioritaires sur l’addition et la soustraction.

Exemple

III- Expressions avec parenthèses

3-1/  Propriété

Dans une suite d’opérations avec parenthèses, on effectue d’abord les calculs entre parenthèses en commençant par les parenthèses les plus intérieures.

Exemple

IV- Distributivité

4-1/  Propriété

Multiplier une somme (ou une différence) par un nombre revient à multiplier chaque terme de la somme (ou de la différence) par ce nombre.

a,b et k sont des nombres décimaux

$$\begin{gathered} \mathrm{k}\times (\mathrm{a}+\mathrm{b})=\mathrm{k}\times \mathrm{a}+\mathrm{k}\times \mathrm{b} \\ \mathrm{k}\times (\mathrm{a}-\mathrm{b})=\mathrm{k}\times \mathrm{a}-\mathrm{k}\times \mathrm{b} \end{gathered}$$

Exemples

V- Exercices

5-1/ Exercice 1

Effectuez les calculs en faisant figurer toutes les étapes du calcul :

V- Exercices

5-2/ Exercice 2

Effectuer les calculs en faisant figurer toutes les étapes du calcul :

V- Exercices

5-3/ Exercice 3

Calculer chaque expression de deux façons :

1. Application de la priorité aux parenthèses.
2. Application de la distributivité.

$$\begin{gathered} A=5\times (3+4) \\ B=6\times (7-4) \\ C=(9+4)\times 2 \\ D=2,5\times (6-4) \\ E=58\times (100+ 2) \\ F=47\times (10-1) \end{gathered}$$

V- Exercices

5-4/ Exercice 4

Utiliser la distributivité pour calculer de façon astucieuse les expressions suivantes :

$$\begin{gathered} A=7\times 5,84-7\times 2,84 \\ B=92\times 101 \\ C=13\times 1894+13\times 106 \\ D=138\times 999 \\ E=157\times 8-7,99\times 157 \end{gathered}$$

V- Exercices

5-5/ Exercice 5

Farid a acheté $8$ stylos et $5$ cahiers.

Soit $x$ le prix en dirhams d'un stylo. Un cahier coûte $10$ dirhams de plus qu'un stylo.

On note $D$ la dépense de Farid en dirhams.

1. Vérifier que $D=8x+5\left(x+10\right)$.

2. Simplifier l'expression de $D$.

3. Sachant que le prix d'un stylo est $4$ dirhams, calculer la dépense de Farid.

V- Exercices

5-6/ Exercice 6

$ABCD$ est un rectangle de périmètre $12,60m$.

On découpe un rectangle $EFGH$ dont les dimensions sont $0,8m$ sur $0,6m$ :

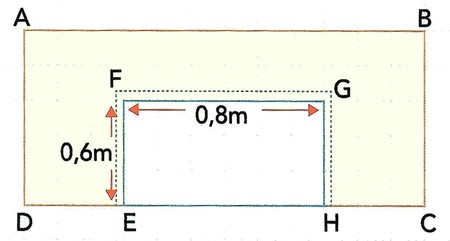
1. Quel est le périmètre de la surface ainsi obtenue ?

Sur le bord de la partie découpée, on découpe maintenant une bande supplémentaire de $10cm$ de large.

2. Quel est le périmètre de la nouvelle surface obtenue ?