
Physique et Chimie : 1ère Année Bac
Séance 29 (Les images formées par une lentille mince convergente)
Professeur : Mr EL GOUFIFA Jihad
Sommaire
I- Généralités sur les lentilles minces
1-1/ Définition d'une lentille sphérique
1-2/ Différents types de lentilles minces
1-3/ Effet d'une lentille mince convergente sur un faisceau lumineux
II- Modélisation et caractéristiques des lentilles convergentes
2-1/ Axe optique principal et centre optique
2-2/ Foyer principal image et foyer principal objet
2-3/ Distance focale et vergence
III- Image formée par une lentille mince convergente
3-1/ Qualité d'une lentille mince convergente
3-2/ Construction de l'image donnée par une lentille mince convergente
IV- Relations de conjugaison et de grandissement
4-1/ Relation de conjugaison de Descartes
4-2/ Relation de grandissement
V- La loupe
5-1/ Définition
5-2/ Construction de l'image donnée par une loupe
VI- Exercices
6-1/ Exercice 1
6-2/ Exercice 2
6-3/ Exercice 3
6-4/ Exercice 4
I- Généralités sur les lentilles minces
1-1/ Définition d'une lentille sphérique
Une lentille est un milieu transparent limité par deux dioptres, les deux peuvent être sphériques ou l’un est sphérique et l’autre est plan (on les nomme souvent lentilles sphériques).
Nous étudierons le cas des lentilles minces : une lentille est mince si son diamètre est très grand devant son épaisseur.

I- Généralités sur les lentilles minces
1-2/ Différents types de lentilles minces
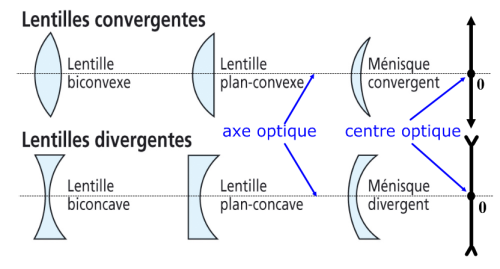
Il existe deux types de lentilles minces :
- Les lentilles à bord mince (convergentes) :
- Les lentilles à bord épais (divergentes) :
I- Généralités sur les lentilles minces
1-3/ Effet d'une lentille mince sur un faisceau lumineux
Les lentilles convergentes transforment le faisceau parallèle de la lampe en un faisceau convergent en un point :

Les lentilles divergentes font diverger, c'est-à-dire s'écarter, le faisceau, et on observe une grosse tache lumineuse :

II- Modélisation et caractéristiques des lentilles convergentes
2-1/ Axe optique principal et centre optique
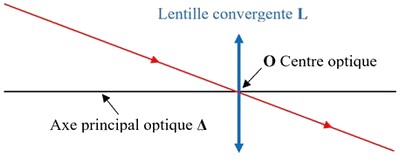
On appelle axe optique principal d'une lentille convergente l'axe de symétrie commun à ses deux faces sphériques et orthogonal à la lentille.
Tout rayon passant par le centre O d'une lentille ne subit aucune dérivation. Ce point O est appelé centre optique de la lentille.
II- Modélisation et caractéristiques des lentilles convergentes
2-2/ Foyer principal image et foyer principal objet
Une lentille convergente comporte deux foyers, appelés foyer principal objet et foyer principal image :
Tout rayon incident parallèle à l’axe principal d’une lentille convergente en émerge en passant par le point F’ appelé foyer principal image de la lentille. Le point F’ est situé après la lentille :
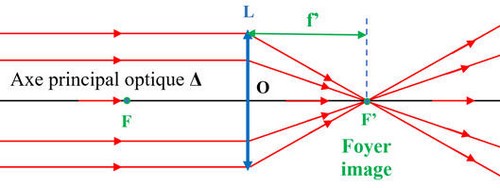
Tout rayon incident passant par le point appelé foyer-objet F émerge de la lentille parallèlement à l’axe optique Δ. Le point F est appelé le foyer principal objet, ce point est réel. Il est situé en avant de la lentille :
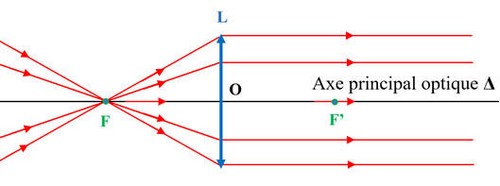
Ces foyers sont symétriques par rapport au centre optique de la lentille.
II- Modélisation et caractéristiques des lentilles convergentes
2-3/ Distance focale et vergence
On appelle distance focale objet la grandeur notée f’ et définie par : f=OF
On appelle distance focale image la grandeur notée f et définie par : f'
On appelle vergence la grandeur notée et définie par . Elle s’exprime en dioptries ou .
III- Image formée par une lentille mince convergente
3-1/ Qualité d'une lentille mince convergente
L'image donnée par la lentille est bonne si elle est nette, non irisée et non déformée.
Pour que la lentille donne une image nette elle doit donner à chaque point A de l'objet un seul point image A' (on dit qu'il y'a stigmatisme rigoureux).
Pour cela il est nécessaire de se trouver dans les conditions de Gauss. Conditions de Gauss:
- 1ère condition : Les rayons lumineux incident doivent être envoyés plus proche du centre optique de la lentille.
- 2ème condition: Les rayons lumineux envoyés par l'objet doivent faire un petit angle avec l'axe optique de la lentille.
Pour réaliser les conditions de Gauss, il suffit d'utiliser un diaphragme devant la lentille.
III- Image formée par une lentille mince convergente
3-2/ Construction de l'image donnée par une lentille mince convergente
Cas ou l'objet est situé à une distance OA>OF
Pour construire l'image d'un objet AB donnée par la lentille, il suffit de tracer les rayons issus de B passant par O, F et F' :
- Tout rayon lumineux issus de B et passant par le centre optique de la lentille n'est pas dévié.
- Tout rayon lumineux issus de B et passant par le foyer principal objet F émerge de la lentille parallèlement à son axe optique.
- Tout rayon lumineux issu de B parallèlement à l'axe optique de la lentille émerge en passant par le foyer principal optique.
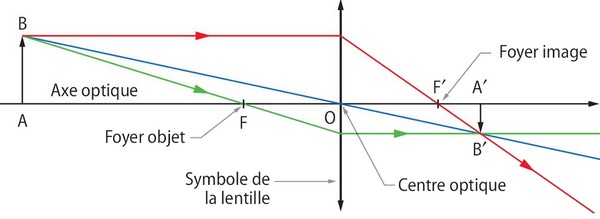
L'objet AB est réel (car il se trouve dans l'espace objet)
L'image A'B' est réelle (car elle se trouve dans l'espace image), et renversée.
III- Image formée par une lentille mince convergente
3-2/ Construction de l'image donnée par une lentille mince convergente
Cas ou l'objet est situé à une distance 0<OA<OF
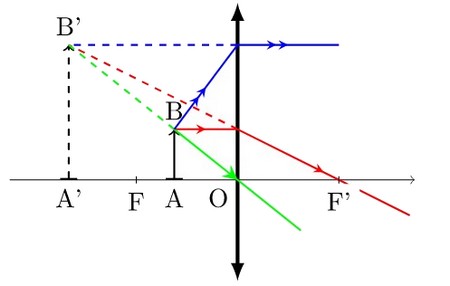
L'objet AB est réel (car il se trouve dans l'espace objet).
L'image A'B' est :
- virtuelle (car elle se trouve dans l'espace objet).
- droite (non renversée).
- plus grande que l'objet.
IV- Relations de conjugaison et de grandissement
4-1/ Relation de conjugaison de Descartes
La position de l’image d’un objet par rapport à une lentille mince convergente ne dépend que de la distance focale f de la lentille : il existe une relation liant la position de l’objet et la position de son image (à travers la lentille convergente), cette relation s’appelle la relation de conjugaison de Descartes :
Si l'objet est réel : , et si l'objet est virtuel :
Si l'image est réelle : , et si l'image est virtuelle :
IV- Relations de conjugaison et de grandissement
4-1/ Relation de conjugaison de Descartes
Démonstration
Les triangles et sont homothétiques (semblables)
Les triangles et sont homothétiques (semblables)
En faisant la somme membre à membre on obtient :
Et on a :
Donc :
IV- Relations de conjugaison et de grandissement
4-2/ Relation de grandissement

Il existe une relation, appelée grandissement, entre la grandeur de l’objet et celle de l’image :
- Si l'objet et l'image ont le même sens, dans ce cas l'image est droite (car elle a le même sens que l'objet) :
- Si l'objet et l'image ont des sens opposés , dans ce cas l'image est renversée :
- Si l'image est plus grande que l'objet :
- Si l'image est plus petite que l'objet :
V- La loupe
5-1/ Définition
La loupe est une lentille mince convergente de faible distance focale (de l'ordre de quelques centimètres).
Dans la vie courante, on utilise une loupe pour observer les objets de petites dimensions.

V- La loupe
5-2/ Construction de l'image donnée par une loupe
La loupe donne d'un objet réel une image virtuelle plus grande que l'objet :
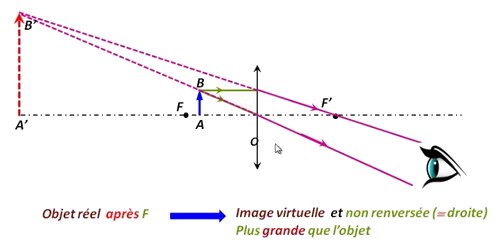
VI- Exercices
6-1/ Exercice 1
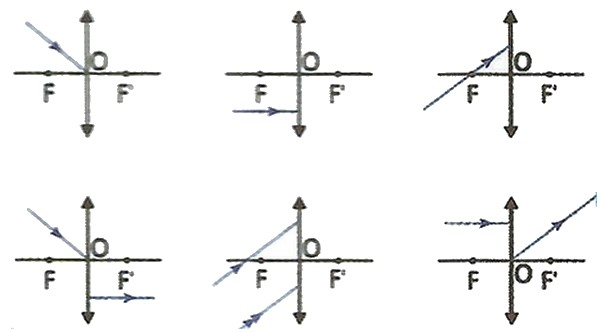
- Reproduire et compléter les schémas suivants, en traçant les rayons incidents ou émergents selon le cas :
VI- Exercices
6-2/ Exercice 2
- Faire la construction graphique, à l’échelle réelle, de l’image d’un objet donnée par une lentille mince convergente de distance focale .
est sur l’axe optique et est perpendiculaire à cet axe.
On donne : et .
- Déterminer graphiquement les caractéristiques de l’image .
- Trouver, par calcul, les valeurs de et .
VI- Exercices
6-3/ Exercice 3
Une lentille mince convergente donne d’un petit objet placé sur l’axe optique une image de même taille :

- Déterminer graphiquement la position du centre optique de la lentille, ainsi que les foyers principaux et .
- En déduire la distance focale de la lentille.
- Quels sont le grandissement et la nature de l’image ?
- Citer une autre méthode de détermination de la distance focale .
VI- Exercices
6-4/ Exercice 4
Un observateur, dont l’œil est placé en est normal, regarde un objet de de hauteur.
Pour distinguer les détails, il utilise une lentille de centre optique et de vergence , qu’il utilise comme loupe.
L’axe optique est confondu avec la droite et l’objet est perpendiculaire à cette droite :
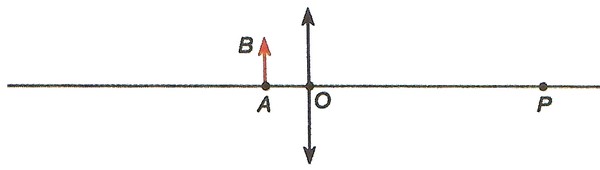
- Calculer la distance focale de cette lentille.
L’observateur place la lentille à de l’objet .
- Déterminer la position de l’image de (on calculera pour cela ). Calculer le grandissement et la taille de l’image,
- Faire un schéma à l’échelle 1 permettant de retrouver les résultats obtenus précédemment.
- Où l’observateur doit- il placer le centre optique de la lentille pour que l’image soit rejetée à l’infini ? Quel est pour l’observateur l’intérêt de cette situation ?


