Séance 11 - Énergie thermique et transfert thermique

Sommaire

I- Transfert d’énergie thermique

1-1/ Notion de transfert thermique

1-2/ Modes du transfert thermique

II- Énergie thermique

2-1/ Définition de l’énergie thermique

2-2/ Capacité thermique massique

2-3/ Équilibre thermique

III- Mesures calorimétriques

3-1/ Détermination de la capacité thermique d’un calorimètre

3-2/ Détermination de la capacité thermique massique d’un corps

IV- Énergie thermique de changement d’état : chaleur latente

4-1/ Les différents changements d'état

4-2/ L’énergie thermique de changement d’état : chaleur latente

V- Exercices

5-1/ Exercice 1

5-2/ Exercice 2

5-3/ Exercice 3

5-4/ Exercice 4

I- Transfert d’énergie thermique

1-1/ Notion de transfert thermique

Lorsque deux corps à des températures différentes sont mis en contact, on constate que la température du corps chaud diminue, tandis que celle du corps froid augmente.

L'énergie interne du corps chaud décroît, celle du corps froid croît.

Il y'a transfert d'énergie entre les deux corps : c'est le transfert thermique noté Q en Joule (J).

I- Transfert d’énergie thermique

1-2/ Modes du transfert thermique

Transfert par conduction

En Chauffant l’une des extrémités d'une barre métallique, on constate réchauffement progressif par conduction le long de la barre.

La conduction est un mode de transfert thermique qui s'effectue sans transport de matière.

I- Transfert d’énergie thermique

1-2/ Modes du transfert thermique

Transfert par convection

Quand on fait bouillir de l'eau dans une casserole, l'eau, chaude par le fond, se dilate puis monte dans la casserole et l'eau froide descend. Il en résulte un mouvement de convection.

La convection est le déplacement sous forme de courant (air chaud : il s'élève au dessus de la source chaude).

La convection est un mode de transfert qui s'effectue avec transport de matière.

I- Transfert d’énergie thermique

1-2/ Modes du transfert thermique

Transfert par rayonnement

Le rayonnement est une autre forme de transfert de la chaleur, il peut se faire sur de très grandes distances et même dans le vide.

Exemple : les ondes électromagnétiques émises par le soleil chauffent la Terre.

I- Transfert d’énergie thermique

1-2/ Modes du transfert thermique

II- Énergie thermique

2-1/ Définition de l’énergie thermique

L'énergie thermique $Q$ est la quantité de chaleur Q reçue ou perdue par un corps de masse $m$ lorsque sa température varie de la température ${\theta }_i$ à la température ${\theta }_f$.

Elle est donnée par la relation suivante :

$\overline{) Q=m.c.\left({\theta }_f-{\theta }_i\right)=\mu .\Delta \theta }$

• $Q$ : énergie thermique en $\left(J\right)$
• $m$ : masse du corps en $\left(kg\right)$
• $c$ : capacité thermique massique du corps en $(J.k{g}^{-1}.K^{-1})$
• $\Delta \theta ={\theta }_f-{\theta }_i$ : variation delà température en $\left(K\right)$
• $\mu =m.c$ : capacité thermique en $(J.K^{-1})$

Si $\Delta \theta >0$, donc $Q>0$ : le corps reçoit la chaleur.

Si $\Delta \theta <0$, donc $Q<0$ : le corps perd la chaleur.

II- Énergie thermique

2-2/ Capacité thermique massique

$Q=m.c.\Delta \theta \Rightarrow c=\frac{Q}{m.\Delta \theta }$

La capacité thermique massique $c$ d’un corps est l’énergie thermique nécessaire pour faire varier de 1°C la température de l’unité de masse (1kg) de ce corps.

$\mu =m.c$ s’appelle la capacité thermique du corps en $(J.K^{-1})$, c'est la quantité de chaleur (énergie thermique) qu’il faut lui fournir pour augmenter sa température de 1°C ou (1°K).

II- Énergie thermique

2-3/ Équilibre thermique

Lorsque deux corps de températures différentes sont mis en contact, le corps le plus froid reçoit de l’énergie du corps le plus chaud par transfert thermique.

Le transfert cesse lorsque les deux corps sont à la même température : on parle alors d’équilibre thermique : $\Delta U=Q=0$.

III- Mesures calorimétriques

3-1/ Détermination de la capacité thermique d’un calorimètre

Les transferts thermiques sont souvent accompagnés de fuites thermiques, pour éviter ces fuites on utilise un calorimètre (c’est une enceinte adiabatique), et de cette façon on réduit les pertes de chaleur.

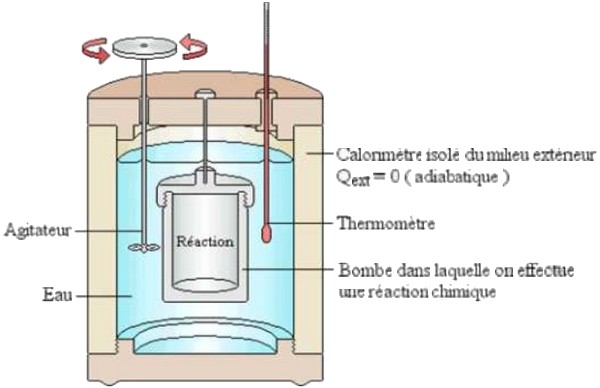
Application

Dans un calorimètre contenant une masse $m_1=300g$ d’eau froide à la température ${\theta }_1=20°C$, on verse rapidement une quantité d’eau chaude de masse $m_2=400g$ et de température ${\theta }_2=61°C$ et la température d’équilibre thermique du mélange se stabilise à la valeur $\theta =42°C$.

On donne la capacité thermique massique de l’eau $c_e=4180J/kg.°C$.

• Déterminer la capacité thermique du calorimètre.

III- Mesures calorimétriques

3-2/ Détermination de la capacité thermique massique d’un corps

Un calorimètre de capacité thermique $\mu =190J/K$ contient une masse $m_1=200g$ d’eau à la température ${\theta }_1=20°C$ de façon que l’ensemble (calorimètre eau) soit en équilibre thermique.

On fait entrer rapidement dans le calorimètre un corps de cuivre de masse $m_C=50g$ et de température ${\theta }_2=70°C$ après l’avoir chauffé dans un bain marie.

La température d’équilibre thermique du mélange se stabilise à la valeur $\theta =20,9°C$.

On donne $c_e=4180J/kg.°C$

• Déterminer la capacité thermique massique du cuivre.

IV- Énergie thermique de changement d’état : chaleur latente

4-1/ Les différents changements d'état

IV- Énergie thermique de changement d’état : chaleur latente

4-2/ L’énergie thermique de changement d’état : chaleur latente

L’énergie thermique de changement d’état (ou chaleur latente ), notée L, est l’énergie qu’il faut fournir à 1 kg d’un corps pur (liquide,solide ou gaz ), à sa température de changement d’état, pour qu’il change d’état.

Exemples :

• chaleur latente de fusion de l’eau glace : $L_{fus}=334.{10}^{3}J.k{g}^{-1}$
• chaleur latente de vaporisation de l’eau liqude : $L_{vap}=2,26.{10}^{6}J.k{g}^{-1}$

Lors de son changement d’état, la masse m d’un corps pur échange avec l’extérieur l’énergie : $Q=m.L_{chang}$

• Q : énergie échangée en joule (J)
• m : masse du corps en kilogramme (kg)
• L : chaleur latente de changement d’état en joule par kilogramme (J∙kg-1)

Pour observer un changement d'état vers une phase moins ordonnée (fusion, vaporisation), le système doit gagner de l’énergie, Q est positive, donc L aussi. La transformation est dite endothermique.

Pour observer un changement d'état vers une phase plus ordonnée (solidification, condensation), le système doit perdre de l’énergie, Q est négative, donc L aussi. La transformation est dite exothermique.

V- Exercices

5-1/ Exercice 1

La capacité thermique massique de l’eau liquide est $c_{eau}=4,18.{10}^{3}J.°C^{-1}.k{g}^{-1}$

La capacité thermique massique de l'aluminium à $c_{Al}=902J.°C^{-1}.k{g}^{-1}$

1. Calculer la variation d'énergie interne de $m_{eau}=200g$ d'eau liquide dont la température passe de $20°C$ à $80°C$.

2. Calculer la variation d'énergie interne de $m_{eau}=600g$ d'eau liquide dans lequel se trouve un morceau d'aluminium de $m_{Al}=250 g$, quand la température de l'ensemble passe de $60°C$ à $10°C$.

3. Ces variations de température étant obtenues par transfert thermique, interpréter le signe des variations d'énergie.

V- Exercices

5-2/ Exercice 2

Le vase calorimétrique d'un calorimètre est en aluminium, sa masse est $m=50g$.

1. Calculer la capacité thermique de ce vase sachant que la capacité thermique massique de l'aluminium vaut $920J.k{g}^{-1}.K^{-1}$.

Le calorimètre contient une masse d'eau de $100g$ ($c_{eau}=4,18.{10}^{3}J.k{g}^{-1}.K^{-1}$), le thermomètre et les accessoires du calorimètre ont une capacité thermique de $15J.K^{-1}$.

2. Calculer la capacité thermique totale $C$ du calorimètre.

La température initiale du calorimètre contenant les $100g$ d’eau est ${\theta }_1=17,2°C$.

On introduit dans le calorimètre une certaine quantité d'eau à la température ${\theta }_2=100°C$, la température d'équilibre s'établit à ${\theta }_{eq}=38,5°C$.

3. Calculer la capacité thermique $C\text{'}$ de l'eau introduite.

4. En déduire la valeur de la masse d'eau.

V- Exercices

5-3/ Exercice 3

On admet que dans un calorimètre, seul le vase intérieur (masse $m_1=300g$, capacité thermique massique $C_1=0,38.kJ.k{g}^{-1}{K}^{-1}$) et l’agitateur (masse $m_2=50g$, capacité thermique massique $C_2=0,90.kJ.k{g}^{-1}{K}^{-1}$) sont susceptibles de participer aux échanges thermiques avec le contenu de l’appareil.

1. Calculer la capacité thermique $\mu$ du calorimètre.

Ce dernier contient $400g$ d’éthanol à la température ${\theta }_1= 17,5°C$ ; on y verse $200g$ d’eau à la température ${\theta }_2= 24,7°C$, et on note la température lorsque l’équilibre thermique est réalisé, soit ${\theta }_e= 20,6°C$.

2. En déduire la valeur de la capacité thermique massique $C$ de l’éthanol.

Donnée :

• Capacité thermique massique de l’eau : $4,19 kJ.k{g}^{-1}{K}^{-1}$.

V- Exercices

5-4/ Exercice 4

Dans un calorimètre en cuivre de masse $m_c=100g$ et qui contient une masse d’eau $m_e=200g$ à ${\theta }_e =4°C$, on introduit une masse $m_1=300g$ de cuivre à ${\theta }_1=-20°C$.

On agite pour atteindre l'équilibre thermique.

1. Calculer la température finale ${\theta }_f$.

2. Montrer que si le cuivre introduit est à la température ${\theta }_2=-50°C$, une partie de l’eau congèle.

3. Calculer la masse de glace formée $m_g$.

Données :

• Chaleurs massiques de cuivre : $395 J.k{g}^{-1}.K^{-1}$
• Chaleur latente de fusion de la glace : $330kJ/kg$