Séance 7 - Équilibre d'un corps sous l'action de 2 forces

Sommaire

I- Équilibre d’un corps sous l’action de deux forces (Rappel)

II- Tension d’un ressort

2-1/ Équilibre d'un corps suspendu à l'extrémité d'un ressort

2-2/ Relation entre la tension et l'allongement du ressort

III- Poussée d’Archimède

3-1/ Définition

3-2/ Mise en évidence de la poussée d'Archimède

3-3/ Caractéristique de la poussée d'Archimède

3-4/ Conditions de flottabilité

IV- Exercices

4-1/ Exercice 1

4-2/ Exercice 2

4-3/ Exercice 3

4-4/ Exercice 4

I- Équilibre d’un corps sous l’action de deux forces (Rappel)

Lorsqu’un solide S soumis à deux forces $\overrightarrow{F_1}$ et $\overrightarrow{F_2}$, il est en équilibre lorsque :

• Les deux forces ont même droite d’action.
• La somme vectorielle des deux forces est nulle : $\overrightarrow{F_1}+\overrightarrow{F_2}=\overrightarrow{0}$.

II- Tension d’un ressort

2-1/ Équilibre d'un corps suspendu à l'extrémité d'un ressort

Système étudié : le corps S

Bilan des forces : le corps S est soumis à l’action de deux forces :

• Force appliquée par le ressort appelé tension du ressort : $\overrightarrow{T}$
• Poids du corps S : $\overrightarrow{P}$

Le corps S est en équilibre $\Rightarrow \overrightarrow{T}+\overrightarrow{P}=0\Rightarrow T=P=m.g$

On appelle allongement du ressort $\Delta \mathcal{l}$ est la différence entre sa longueur finale et sa longueur initiale : $\Delta \mathcal{l}=\mathcal{l}-{\mathcal{l}}_0$

II- Tension d’un ressort

2-2/ Relation entre la tension et l'allongement du ressort

On suspend successivement différentes masses marquées à un ressort de longueur initiale l0=10cm , et on mesure sa longueur finale pour chaque équilibre.

Puis on trace la courbe qui représente la variation de $T$ en fonction de l'allongement $\Delta \mathcal{l}$.

On prend $g=10N/kg$

Tableau des mesures :

Courbe $T=f\left(\Delta \mathcal{l}\right)$ :

La courbe est linéaire, son équation s’écrit : $T=K.\Delta \mathcal{l}$

$K$ représente la constante de raideur du ressort $K=\frac{0,4}{4.{10}^{-2}}=10N.m^{-1}$.

La tension du ressort s’écrit :

III- Poussée d’Archimède

3-1/ Définition

Tout corps immergé (partiellement ou totalement) dans un fluide (gaz ou liquide) subit de la part de ce fluide une force de contact répartie appelée poussée d'Archimède.

III- Poussée d’Archimède

3-2/ Mise en évidence de la poussée d'Archimède

Expérience

On suspend un corps solide à un dynamomètre, on note la valeur $T$ affichée du dynamomètre.

On immerge le solide suspendue dans l’eau, le dynamomètre indique la valeur $T\text{'}<T$.

Dans l’air le solide est en équilibre sous l’action de 2 forces : $T=P=5N$

Dans l’eau le solide est en équilibre sous l’action de 3 forces :

$P-T\text{'}-F_A=0\Rightarrow F_A=P-T\text{'}=2N$

Le poids de l’eau déplacé est :

$P_{eau}=\rho .V_{eau}.g={10}^3.2.{10}^{-4}.9,8\approx 2N$

Donc on a : $\overline{) F_A=P_{eau} }$

III- Poussée d’Archimède

3-2/ Mise en évidence de la poussée d'Archimède

Conclusion

Tout corps plongé dans un fluide (liquide ou gaz) au repos, subit de la part de ce fluide une force de poussée verticale, dirigée vers le haut, et dont l’intensité est égale au poids de volume de fluide déplacé.

III- Poussée d’Archimède

3-3/ Caractéristique de la poussée d'Archimède

• Point d’application : centre d’inertie du fluide déplacé (centre du volume immergé).
• Droite d’action : la verticale passant par le centre de la poussée.
• Sens : du bas vers le haut.
• Intensité : du poids du fluide déplacé $F_A=\rho .g.V$

III- Poussée d’Archimède

3-4/ Conditions de flottabilité

La « flottabilité » caractérise le comportement d’un objet immergé au sein d’un liquide.

Un objet immergé dans un fluide (liquide ou gaz) est soumis à deux forces de sens contraire :

• son poids $\overrightarrow{P}$
• la poussée d’Archimède $\overrightarrow{F_A}$

Si $P>F_A$ (ou ${\rho }_{objet}>{\rho }_{fluide}$) : l’objet coule vers le fond.

Si $P=F_A$ (ou ${\rho }_{objet}={\rho }_{fluide}$) : l’objet est en équilibre et flotte entre deux eaux (flotter légèrement sous la surface)

Si $P<F_A$ (ou ${\rho }_{objet}<{\rho }_{fluide}$) : l’objet remonte vers la surface, il flotte à la surface et en équilibre lorsque l’intensité de la poussée d’Archimède deviendra égale au poids de l’objet.

IV- Exercices

4-1/ Exercice 1

Soit un corps $S$, de masse $m$ inconnue, maintenu en équilibre sur un plan incliné sans frottement par un ressort.

Le plan incliné fait un angle $\alpha =20°$ avec l’horizontal et la raideur du ressort est $k=15N.m^{-1}$.

1. Faire un schéma de la situation.

2. Définir le système et faire le bilan des forces qui s’y exercent.

3. Calculer la valeur de la force exercée par le ressort sur le corps $S$ (tension de ressort $T$) sachant que son allongement est de $\Delta l=5cm$.

IV- Exercices

4-2/ Exercice 2

Un cube homogène, d’arête a égale à $10cm$, est fabriqué dans un matériau de masse volumique ${\rho }_C$, immergé dans l’eau et suspendu à un ressort vertical de constante de raideur $K=200N.m^{-1}$ en B, le centre d’une face ; il est en équilibre.

1. Déterminer les valeurs du poids $P$ du cube et de la poussée d’Archimède $F_A$ exercée par l’eau sur le solide.

Le solide étant en équilibre, les forces extérieures appliquées à ce cube sont colinéaires et leur direction passe par $G$ centre d’inertie du cube.

2. Déterminer la valeur de la force de rappel $T$ du ressort.

3. Représenter les trois forces s’exerçant sur le solide à une échelle convenable.

4. Déterminer l’allongement du ressort.

Données :

• $g=10 N.k{g}^{-1}$
• ${\rho }_C=9,0.{10}^{3}kg.m^{-3}$

IV- Exercices

4-3/ Exercice 3

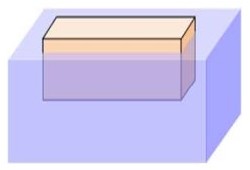
Un pavé flotte à la surface de l’eau. Ses dimensions sont :

• hauteur : $20cm$
• longueur : $60cm$
• largeur : $20cm$

Le pavé émerge sur une hauteur de $3cm$.

1. Calculer le volume de la partie immergée.

2. Calculer la masse d’eau déplacée.

3. Calculer le poids d’eau déplacé, et en déduire la valeur du poids du pavé.

4. Calculer la masse du pavé.

5. Calculer le volume du pavé.

6. Préciser le matériau constituant ce pavé :

Données :

• $g=10 N.k{g}^{-1}$
• Masse volumique de l’eau : $\rho ={10}^{3}Kg.m^{-3}$

IV- Exercices

4-4/ Exercice 4

On dispose d'un ressort à spires non jointives, parfaitement élastique, de longueur au repos lorsqu'il n'est pas déformé $L_0=10cm$ et de raideur $k=80N.m^{-1}$.

On accroche une extrémité du ressort à une potence, puis on tire sur l'autre extrémité avec une force de valeur $F=4,0N$.

1. Quelle est la longueur $L$ prise par le ressort ?

2. Quelle est la valeur $F\text{'}$ de la force exercée quand le ressort a une longueur $L\text{'}=12cm$ ?

3. Quelle est la raideur d'un ressort qui prend la longueur $L\text{'}=12cm$ quand on exerce sur son extrémité libre la force de valeur $F=4,0N$ ? (Ce ressort a la même longueur au repos que le précédent.)