
Mathématiques : 2Bac SMA-SMB
Séance 2-2-1 : Suites numériques - Partie 2 (Cours)
Professeur : Mr CHEDDADI Haitam
Sommaire
III- Limite d’une suite numérique
3-1/ Suite de limite infinie
3-2/ Limite infinie des suites usuelles
3-3/ Convergence d'une suite numérique
3-4/ Convergence des suites usuelles
3-5/ Unicité de la limite
3-6/ Opérations sur les limites
3-7/ Extension des opérations sur la limite de suite
3-8/ Limites et ordre
3-9/ Monotonie et convergence
IV- Critères de convergence
4-1/ Existence de la limite par encadrement
4-2/ Limite d'une suite géométrique
III- Limite d’une suite numérique
3-1/ Suite de limite infinie
Définition 5
On dit que la suite a pour limite si tout intervalle de type , où , contient tous les termes de la suite à partir d'un certain rang, ce qui revient à dire que :
On dit alors que la suite diverge vers , et on notera :
On dit que la suite a pour limite si tout intervalle de type contient tous les termes de la suite à partir d’un certain rang ; ce qui revient à dire que :
On dit alors que la suite diverge vers , et on notera :
III- Limite d’une suite numérique
3-1/ Suite de limite infinie
Remarques
Si , alors on a l'implication :
On a les équivalences suivantes :
III- Limite d’une suite numérique
3-2/ Limite infinie des suites usuelles
Proposition 1
Les suites , , et tendent vers quand tend vers .
III- Limite d’une suite numérique
3-2/ Limite infinie des suites usuelles
Proposition 2
Soit et deux suites numériques telles que pour tout :
Si , alors .
Si , alors .
III- Limite d’une suite numérique
3-2/ Limite infinie des suites usuelles
Proposition 3
Soit un réel quelconque.
Si alors .
Si alors .
III- Limite d’une suite numérique
3-2/ Limite infinie des suites usuelles
AppIications
Déterminer les limites suivantes :
III- Limite d’une suite numérique
3-3/ Convergence d'une suite numérique
Définition 6
Étant donné une suite numérique et , on dit que tend vers , ou encore converge vers , si tout intervalle ouvert centré en contient tous les termes de la suite à partir d’un certain rang.
En d’autres termes :
Et on écrit :
III- Limite d’une suite numérique
3-3/ Convergence d'une suite numérique
Définition 7
On dit qu’une suite numérique est convergente si elle admet une limite réelle.
Dans le cas contraire, on dit qu’elle est divergente.
III- Limite d’une suite numérique
3-3/ Convergence d'une suite numérique
Remarque
Dire qu'une suite diverge (ou qu'elle est divergente), ne signifie pas qu'elle tend vers l'infini.
Cela signifie exactement que la suite n'a pas de limite ou qu'elle tend vers l'infini.
III- Limite d’une suite numérique
3-3/ Convergence d'une suite numérique
AppIications
Soit la suite numérique définie par .
- Montrer en utilisant la définition que .
On considère les deux suites et définies par et .
- Montrer en utilisation la définition que et .
III- Limite d’une suite numérique
3-4/ Convergence des suites usuelles
Proposition 4
Les suites , et tendent vers quand tend vers .
III- Limite d’une suite numérique
3-5/ Unicité de la limite
Proposition 5
La limite d’une suite numérique, lorsqu’elle existe, est unique.
III- Limite d’une suite numérique
3-5/ Unicité de la limite
Proposition 6
Toute suite convergente est bornée. La réciproque est fausse.
III- Limite d’une suite numérique
3-6/ Opérations sur les limites
Proposition 7
Soit et deux suites numériques convergentes. Alors :
La suite est convergente, et de plus : .
La suite est convergente, et de plus : .
Si , alors la suite est convergente, et de plus : .
III- Limite d’une suite numérique
3-6/ Opérations sur les limites
Applications
Calculer la limite de chacune des suites suivantes définies par :
III- Limite d’une suite numérique
3-7/ Extension des opérations sur la limite de suite
On admet que les résultats sur les limites des fonctions restent valables pour les limites des suites :
- Limite d’une somme :
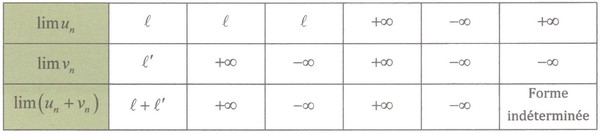
- Limite d'un produit :
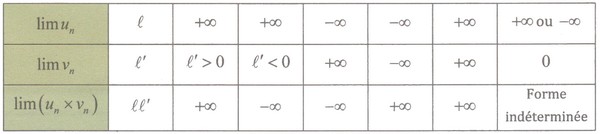
- Limite d’une inverse :
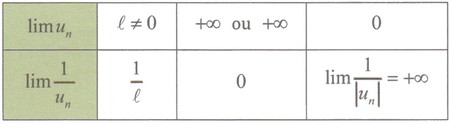
III- Limite d’une suite numérique
3-8/ Limites et ordre
Proposition 8
Soit et deux suites convergentes. Alors :
Si la suite est positive, alors .
Si pour tout entier , alors .
III- Limite d’une suite numérique
3-8/ Limites et ordre
Remarque
Si est une suite convergente dont on souhaite montrer que sa limite est strictement positive, alors il suffit de chercher un réel tel que à partir d'un certain rang.
III- Limite d’une suite numérique
3-9/ Monotonie et convergence
Théorème 1
Toute suite croissante majorée est convergente.
Toute suite décroissante minorée est convergente.
Ce résultat porte le nom de «Théorème de la convergence monotone».
III- Limite d’une suite numérique
3-9/ Monotonie et convergence
Remarque
Le théorème de la convergence monotone assure la convergence de la suite mais ne détermine pas sa limite.
III- Limite d’une suite numérique
3-9/ Monotonie et convergence
Applications
- Montrer que la suite définie par et pour tout : , est décroissante et minorée par .
- Que peut-on en déduire quant à la convergence de la suite ?
Soit la suite numérique définie par :
- Montrer que pour tout entier : . En déduire que la suite est majorée.
- Montrer que la suite est croissante puis en déduire qu'elle est convergente.
III- Limite d’une suite numérique
3-9/ Monotonie et convergence
Proposition 9
Toute suite croissante non majorée tend vers .
Toute suite décroissante non minorée tend vers .
IV- Critères de convergence
4-1/ Existence de la limite par encadrement
Théorème 2
Soit et deux suites numériques convergeant vers une limite commune .
Si est une suite vérifiant l'encadrement à partir d'un certain rang, alors la suite converge et sa limite vaut .
Ce résultat est appelé «Théorème des gendarmes»
IV- Critères de convergence
4-1/ Existence de la limite par encadrement
Applications
Soit la suite numérique définie par :
- Déterminer la limite de la suite .
- Calculer les limites des suites et définies par : et .
IV- Critères de convergence
4-1/ Existence de la limite par encadrement
Corollaire
Soit une suite numérique et un nombre réel.
S'il existe une suite tendant vers telle que pour tout , , alors la suite converge et sa limite vaut .
IV- Critères de convergence
4-1/ Existence de la limite par encadrement
Proposition 10
Soit un nombre rationnel non nul.
Si alors .
Si alors .
IV- Critères de convergence
4-2/ Limite d'une suite géométrique
Soit un nombre réel non nul.
- Si alors .
- Si alors .
- Si alors .
- Si alors la suite n’admet pas de limite.


